filmov
tv
Introduction to Square Roots

Показать описание
Introduction to square roots | Numbers and operations | 8th grade | Khan Academy
What are Square Roots? | Math with Mr. J
Introduction to Square Roots
Introduction to Square Roots
Introducing Square Root
Math Antics - Exponents and Square Roots
THE SQUARE ROOT 🚀 What is the Square Root? 👨🏻🚀 Math for Kids
Why is it called a SQUARE root?
Squares and square roots/ Class 8th / Introduction/ Lecture 1 / Part 1 /@arfatmathsclasses5723
What is a Square Root and a Perfect Square?
Understanding square roots | Pre-Algebra | Khan Academy
How To Simplify Square Roots
Art of Problem Solving: Square Root Introduction Part 1
Math Antic - Simplifying Square Roots
Introduction to Square Roots With Area
Square Roots | Intro, Perfect Squares, and Simplifying | Math with Mr. J
Square Roots and Cube Roots | Math with Mr. J
What are Square Roots? | Exponents | Best Square Root Tricks | Don't Memorise
Introduction - Squares & Square Roots, Ch 5 - NCERT Class 8 Maths Solutions
Grade 8 | Maths | Square and square roots | Free Tutorial | CBSE | ICSE | State Board
Introduction to Square Roots | Number & Operations | 8th Grade
Simplifying square roots | Exponents, radicals, and scientific notation | Pre-Algebra | Khan Academy
Square roots and real numbers | Pre-Algebra | Khan Academy
01 - Simplify Square Roots with Factor Trees in Algebra (Radical Expressions), Part 1
Комментарии
 0:05:23
0:05:23
 0:04:00
0:04:00
 0:07:04
0:07:04
 0:04:14
0:04:14
 0:03:49
0:03:49
 0:11:09
0:11:09
 0:05:13
0:05:13
 0:03:03
0:03:03
 0:11:37
0:11:37
 0:06:38
0:06:38
 0:01:21
0:01:21
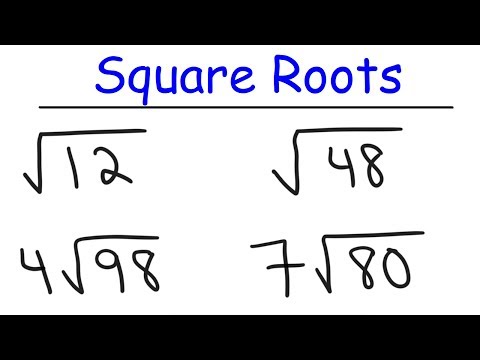 0:10:46
0:10:46
 0:05:17
0:05:17
 0:12:01
0:12:01
 0:04:37
0:04:37
 0:16:35
0:16:35
 0:05:03
0:05:03
 0:04:11
0:04:11
 0:27:17
0:27:17
 0:07:03
0:07:03
 0:07:25
0:07:25
 0:03:09
0:03:09
 0:10:19
0:10:19
 0:43:40
0:43:40