filmov
tv
Integral sqrt(x^2+1)

Показать описание
In this video, the second one of the trig integration trilogy (the first one being the square root of 1-x^2), I find an antiderivative of the square root of x^2 + 1 using a trig substitution. Along the way, I also find an antiderivative of sec^3(x). Enjoy!
Integral of sqrt(x^2+1), integral of sqrt(x^2-1), integral of sqrt(1-x^2)
integral of sqrt(x^2+1), with Euler Substitution, math for fun
Integral sqrt(x^2+1)
Integral of sqrt(x^2-1)
a hard integral of sqrt(x^2-1), trig substitution, calculus 2 tutorial
Trigonometric substitution for a definite integral sqrt(x^2-1)/x^2 on [1,2].
Integral of sqrt(x^2-1)/x (substitution)
integral of sqrt(1-x^2), trig substitution, calculus 2 tutorial
Calculus 2 Exam Review Part6
Integral sqrt(1-x^2)
integral of sqrt(1+x^2), trig substitution, calculus 2 tutorial
Integral of x*sqrt(1-x^2) vs. integral of sqrt(1-x^2), u-substitution vs. integration by parts
hyperbolic substitution, integral of sqrt(1+x^2)
integrate sqrt(x+1) over sqrt(x+2)
Integral of x/sqrt(1-x^2)
Integral of sqrt(1-x^2)
Weird u-substitution for the integral of sqrt(1+x^2)
int (ln (x+sqrt(x^2 -1))
Evaluate the Integral (sqrt(1+x^2))/x dx Trigonometric Substitution.
integral of sqrt(1+x^2)/x vs integral of x/sqrt(1+x^2)
Find Antiderivative of integral x sqrt(x^2 +1) dx using variable substitution
Integral of 1/sqrt(1-x^2)
First 2 Trigonometric Substitution Examples: Integral of Sqrt(1-x^2) and Integral of Sqrt(1+x^2)
integral of 1/(x^2*sqrt(x^2-1), trig substitution, calculus 2 tutorial.
Комментарии
 0:17:27
0:17:27
 0:20:42
0:20:42
 0:10:22
0:10:22
 0:06:27
0:06:27
 0:02:56
0:02:56
 0:07:12
0:07:12
 0:03:02
0:03:02
 0:03:41
0:03:41
 5:47:36
5:47:36
 0:11:01
0:11:01
 0:02:36
0:02:36
 0:09:15
0:09:15
 0:08:11
0:08:11
 0:15:00
0:15:00
 0:03:19
0:03:19
 0:03:45
0:03:45
 0:01:21
0:01:21
 0:10:02
0:10:02
 0:06:45
0:06:45
 0:11:51
0:11:51
 0:03:49
0:03:49
 0:02:56
0:02:56
 0:24:51
0:24:51
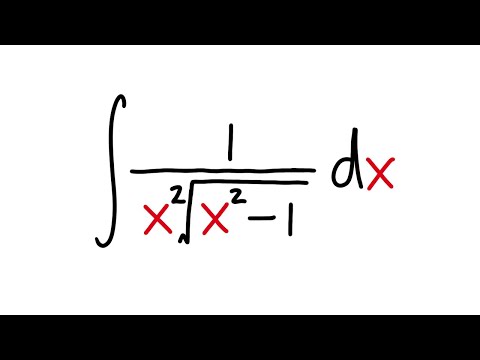 0:04:23
0:04:23