Integral sqrt(1-x^2)

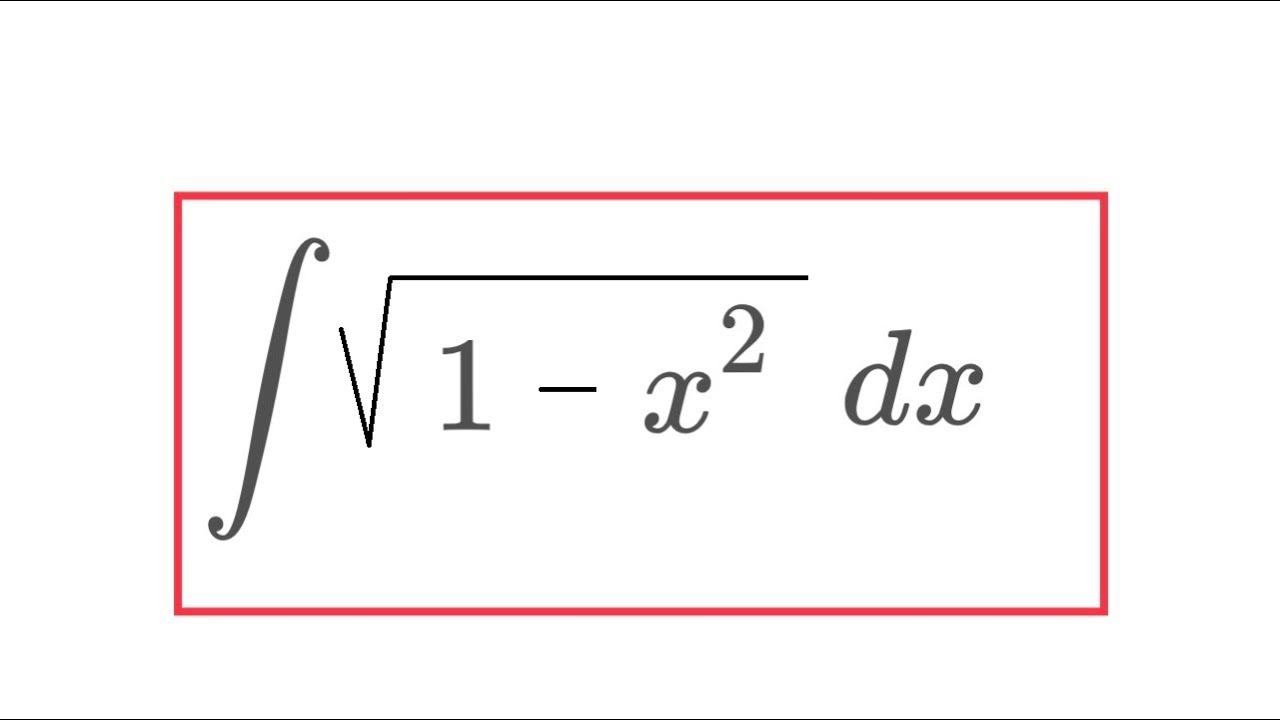
Показать описание

In this video I calculate an antiderivative of the square root of 1-x^2 using trigonometric substitution (and the triangle method) and along the way I also calculate an antiderivative of cos^2(x). Enjoy!

Small correction: It should be [-pi/2,pi/2], not (-pi/2,pi/2)

Рекомендации по теме

Комментарии

You can use this to proof the equation for the area of a circle

helloitsme

Using the substitution x=cos(theta) for theta in domain (0, pi) the integral becomes + C, which differs by the answer in the video by the constant pi/4 :)

KyuuleGamingHD

It really does imply some kind of trigonometry since if you note y=sqrt(1-x^2),
then you have y^2 = 1 - x^2 and you get x^2 + y^2 = 1, the equation of the trigonometric circle !
Which motivate even more using x=sin(theta) or x=cos(theta).

xavierplatiau

How to solve it with no u-sub at all!
B = INT sqrt(1-x^2) = INT = INT 1/sqrt(1-x^2) + INT -x^2/sqrt(1-x^2) = arcsin(x) + INT x*(-x/sqrt(1-x^2)) = B
Let's integrate by parts:
INT x*(-x/sqrt(1-x^2)) = x*sqrt(1-x^2) - INT sqrt(1-x^2) = x*sqrt(1-x^2) - B

So 2B= arcsin(x) + x*sqrt(1-x^2), hence B=(1/2)*[arcsin(x) + x*sqrt(1-x^2)]
As Dr. Peyam would say...TADAN!

Zonnymaka

He's so happy while explainning, that makes me happy too!

mariaclarascarpellipereira

sqrt(1-x^2) = cos(arcsin(x)) = sin(arccos(x)) to make that problem harder for students.

PackSciences

My favorite way to do integrals like this one is by using integration by parts. I won't spoil the solution, go try it out for yourself :) I find that I can use integration by parts to evaluate almost any integral that can be evaluated using trig sub. Try integrating x²/(x²+1)² using integration by parts as well. That's another good example.

violintegral

I'm from hyd! India! Loved how ardently u taught

aishakhan

You're the best, Dr Peyam! <3

cycklist

I only just noticed you're left-handed! wow! (welcome to the club)

MrRyanroberson

We could also say that since the domain of the integrand is -1 ≤ x ≤ 1, then theta should be between -pi/2 and pi/2.

sujitsivadanam

You're amazing.
The part in you say "abracadabra, socatoa" was very funny.

VortexGamesYT

I love your channel and Black Pen Red Pen. You two are treasures.

thomaskotch

Hey! Not only Americans watch you! UK here checking in.

cycklist

You can also solve this integral geometrically.

chiprollinson

oh my god.. i was so bored of math and then this video started 🥰🥰

nehagautam

It's been a while since I've done trig sub (doesn't come up much in my EE courses); why did we want sin(x) to be one-to-one when we made the initial substitution?

justanothergirl__

Love your enthusiasm! Thank you so much for helping me!

Tealsquiddev

anyone else here for finding a formula that discribes pi? :)
pi = 2*arcsin(1) !!!

ShadowZZZ

Quite curiously, I got thorough with trigonometry whilst going through calculus

aryanks

Integral sqrt(1-x^2)

integral of sqrt(1-x^2), trig substitution, calculus 2 tutorial

integral of sqrt(1+x^2), trig substitution, calculus 2 tutorial

hyperbolic substitution, integral of sqrt(1+x^2)

Integral sqrt(1-x^2)

Integral of sqrt(x^2+1), integral of sqrt(x^2-1), integral of sqrt(1-x^2)

Integral of 1/sqrt(1-x^2)

Evaluate the Integral (sqrt(1+x^2))/x dx Trigonometric Substitution.

Weird u-substitution for the integral of sqrt(1+x^2)

Prove lim(xn) = 0 for the sequence x0 = x, xn+1 = xn / (1 + sqrt(1+xn^2)) (ILIEKMATHPHYSICS)

Integral with square root of (1- x^2)

Let me quickly integrate x/sqrt(1-x^2)

Integral of sqrt(1-x^2)

Integral of x*sqrt(1-x^2) vs. integral of sqrt(1-x^2), u-substitution vs. integration by parts

integral of sqrt(1+x^2)/x vs integral of x/sqrt(1+x^2)

Steps to Understand Substitution Method to Integrate sqrt(1 + x^2) x^5

integral of sqrt(x^2+1), with Euler Substitution, math for fun

How REAL Men Integrate Functions

First 2 Trigonometric Substitution Examples: Integral of Sqrt(1-x^2) and Integral of Sqrt(1+x^2)

Trigonometric substitution for a definite integral sqrt(x^2-1)/x^2 on [1,2].

Integral sqrt(x^2+1)

Integral of x/sqrt(1-x^2)

Trig Substitution to find Integral sqrt 1-x^2 AP Calculus Trigonometric Substitution

Integral of 1/(x^2)sqrt(1-x^2) (substitution)

The Integral of sqrt(1-x^2) from 0 to 1 Using U-Substitution