filmov
tv
integral of sqrt(1+x^2)/x vs integral of x/sqrt(1+x^2)

Показать описание
NOTE: it's possible to do u sub for the integral of sqrt(1+x^2)/x as well. Thanks to usuario0002hotmail for pointing out.
, trig substitution, calculus 2 tutorial.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
, trig substitution, calculus 2 tutorial.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
integral of sqrt(1+x^2)/x vs integral of x/sqrt(1+x^2)
Integral of x*sqrt(1-x^2) vs. integral of sqrt(1-x^2), u-substitution vs. integration by parts
integral of sqrt(1-x^2), trig substitution, calculus 2 tutorial
Q6, integral of 1/sqrt(1-x^2) vs. integral of x/sqrt(1-x^2)
Steps to Understand Substitution Method to Integrate sqrt(1 + x^2) x^5
integral of sqrt(1+x^2), trig substitution, calculus 2 tutorial
Evaluate the Integral (sqrt(1+x^2))/x dx Trigonometric Substitution.
Integral of sqrt(1-2x)
Integral of sqrt(x^2+1), integral of sqrt(x^2-1), integral of sqrt(1-x^2)
Let me quickly integrate x/sqrt(1-x^2)
Integral sqrt(1-x^2)
hyperbolic substitution, integral of sqrt(1+x^2)
1 minute integral vs. 9 minutes integral, trig sub, calculus 2 tutorial
Integral of x/sqrt(1-x^2)
Weird u-substitution for the integral of sqrt(1+x^2)
Integral of sqrt(1+e^x) - Integral example
integral of 1/(x^2*sqrt(x^2-1), trig substitution, calculus 2 tutorial.
Integral of e^sqrt(x)
world’s fastest calculus teacher
Integral of sqrt(1-x^2)
Integral of 1/sqrt(1-x^2)
Integral of 1/sqrt(1 - x^2)
integral of sqrt(x^2+1), with Euler Substitution, math for fun
Integral 1/(x-1)sqrt(x^2-2x)
Комментарии
 0:11:51
0:11:51
 0:09:15
0:09:15
 0:03:41
0:03:41
 0:03:40
0:03:40
 0:06:26
0:06:26
 0:02:36
0:02:36
 0:06:45
0:06:45
 0:01:40
0:01:40
 0:17:27
0:17:27
 0:01:01
0:01:01
 0:11:01
0:11:01
 0:08:11
0:08:11
 0:10:32
0:10:32
 0:03:19
0:03:19
 0:01:21
0:01:21
 0:03:37
0:03:37
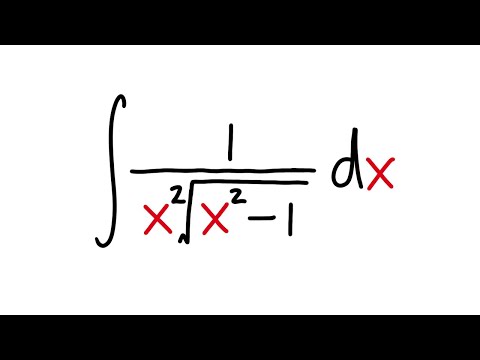 0:04:23
0:04:23
 0:05:43
0:05:43
 0:00:59
0:00:59
 0:03:45
0:03:45
 0:02:56
0:02:56
 0:03:16
0:03:16
 0:20:42
0:20:42
 0:02:16
0:02:16