filmov
tv
Linear Algebra: Linear Systems and Matrix Algebra (full lecture)

Показать описание
We introduce the rank of a matrix and matrix algebra including the product of a matrix and a vector.
Introduction to Linear Algebra: Systems of Linear Equations
Linear Algebra 1.1.1 Systems of Linear Equations
Gaussian Elimination & Row Echelon Form
Linear Algebra - 27 - Algebraic Systems of Equations with Matrices
Linear Algebra - Solving Systems of Equations
Linear Algebra 1: Systems of linear equations - Oxford Mathematics 1st Year Student Lecture
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
What is a Solution to a Linear System? **Intro**
Systems of Linear Equations - Part Two | Linear Algebra Entire Course
How do we solve a system of linear equations using any method
How to Solve Linear Equations With Variables on Both Sides : Linear Algebra Education
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear Algebra - Lecture 7 - Linear Combinations and Vector Equations
Consistency of a System of Linear Equations
Homogenous Linear Systems, Trivial and Nontrivial Solutions | Linear Algebra
Linear Equations - Algebra
Linear Algebra: Introduction to Systems of Linear Equations (Section 1.1) | Math with Professor V
Introduction to Systems of Linear Equations (TTP Video 47)
Linear Algebra: Introduction to Linear Systems (Full Lecture)
Linear Algebra - Lecture 10 - Homogeneous Linear Systems
Geometry of Linear Algebra
1.1 - Introduction to Systems of Linear Equations (Part 1)
Linear Algebra - Introduction to linear systems
How To Solve Linear Equations In Algebra
Комментарии
 0:10:45
0:10:45
 0:18:18
0:18:18
 0:18:40
0:18:40
 0:07:18
0:07:18
 0:05:59
0:05:59
 0:51:36
0:51:36
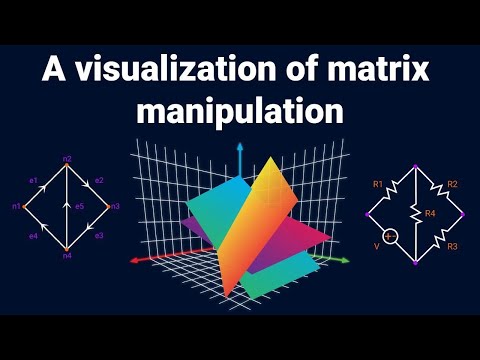 0:16:26
0:16:26
 0:05:28
0:05:28
 0:25:24
0:25:24
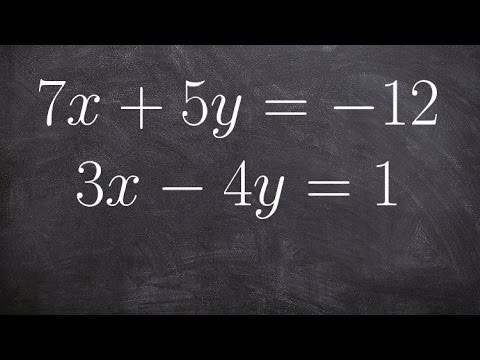 0:04:34
0:04:34
 0:01:54
0:01:54
 0:10:59
0:10:59
 0:08:10
0:08:10
 0:03:11
0:03:11
 0:09:57
0:09:57
 0:32:05
0:32:05
 0:26:08
0:26:08
 0:17:32
0:17:32
 0:41:07
0:41:07
 0:08:54
0:08:54
 0:16:36
0:16:36
 0:21:45
0:21:45
 0:17:59
0:17:59
 0:19:38
0:19:38