filmov
tv
Matrices, matrix multiplication and linear transformations | Linear algebra makes sense

Показать описание
Next video:
Matrices are often presented as a useful bookkeeping/ commutation tools to students- but there’s much more to them. When you understand what a Matrix really is so many parts of Linear Algebra will be completely obvious to you… including the formula for matrix multiplication and the fact that matrices don’t commute. So here's the big secret: A matrix is a linear transformation that eats a vectors and outputs another vector.
Homework questions:
Not all sized matrices can be multiplied together. Think about it in terms of them representing transformations from one space to another, and figure out which size matrices can be multiplied and explain why in the comments.
Music: Epidemic sound, Summer nights 2
This video is an Introduction to Matrices but could be useful revision for school/university. If you have an exam, good luck!
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
How to Multiply Matrices with Rabbits #SoME3
Multiplying Matrices
Multiplying a matrix by a matrix | Matrices | Precalculus | Khan Academy
How To Multiply Matrices - Quick & Easy!
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Intro to Matrices
Matrices, matrix multiplication and linear transformations | Linear algebra makes sense
2024-Q4-AI 2. Matrix transformations, Linear algebra, OOP
Matrix Multiplication and Associated Properties
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
Linear Algebra - Matrix Operations
How to organize, add and multiply matrices - Bill Shillito
Why do we multiply matrices the way we do??
Understanding Matrices and Matrix Notation
Visualize Different Matrices part1 | SEE Matrix, Chapter 1
How AI Discovered a Faster Matrix Multiplication Algorithm
[Linear Algebra] Matrix Multiplication
Multiplying a matrix by a column vector | Matrices | Precalculus | Khan Academy
3.1.18-Linear Algebra: Permutation Matrix Left vs. Right Multiplication
Scalar Multiplication of Matrices and Matrix Operations
But what are Matrices, really? | Linear Algebra Explained
Linear Algebra - Lecture 12: Block Matrices
Tate explains matrices in 90 seconds
Комментарии
 0:10:04
0:10:04
 0:00:47
0:00:47
 0:17:40
0:17:40
 0:05:29
0:05:29
 0:10:48
0:10:48
 0:10:59
0:10:59
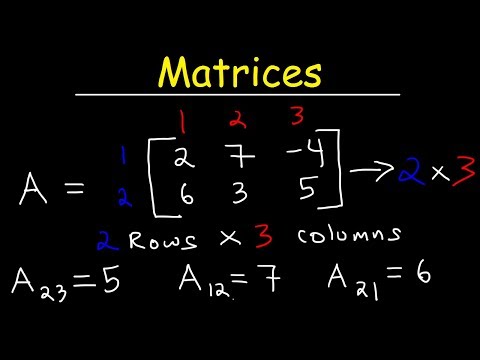 0:11:23
0:11:23
 0:14:06
0:14:06
 2:23:10
2:23:10
 0:06:22
0:06:22
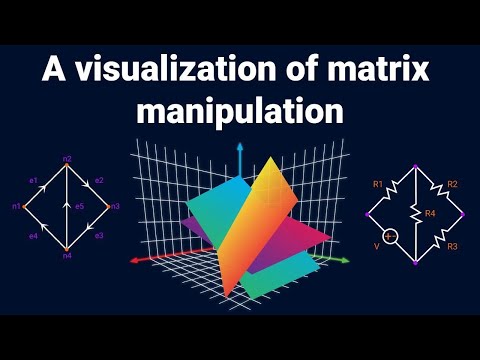 0:16:26
0:16:26
 0:07:08
0:07:08
 0:04:41
0:04:41
 0:16:26
0:16:26
 0:05:26
0:05:26
 0:14:51
0:14:51
 0:13:00
0:13:00
![[Linear Algebra] Matrix](https://i.ytimg.com/vi/Hm5M2jvFJug/hqdefault.jpg) 0:19:02
0:19:02
 0:03:57
0:03:57
 0:00:58
0:00:58
 0:06:37
0:06:37
 0:15:10
0:15:10
 0:17:37
0:17:37
 0:01:30
0:01:30