filmov
tv
Can Calculus Help Solve IMO Problems? | International Mathematical Olympiad 1976 Problem 4
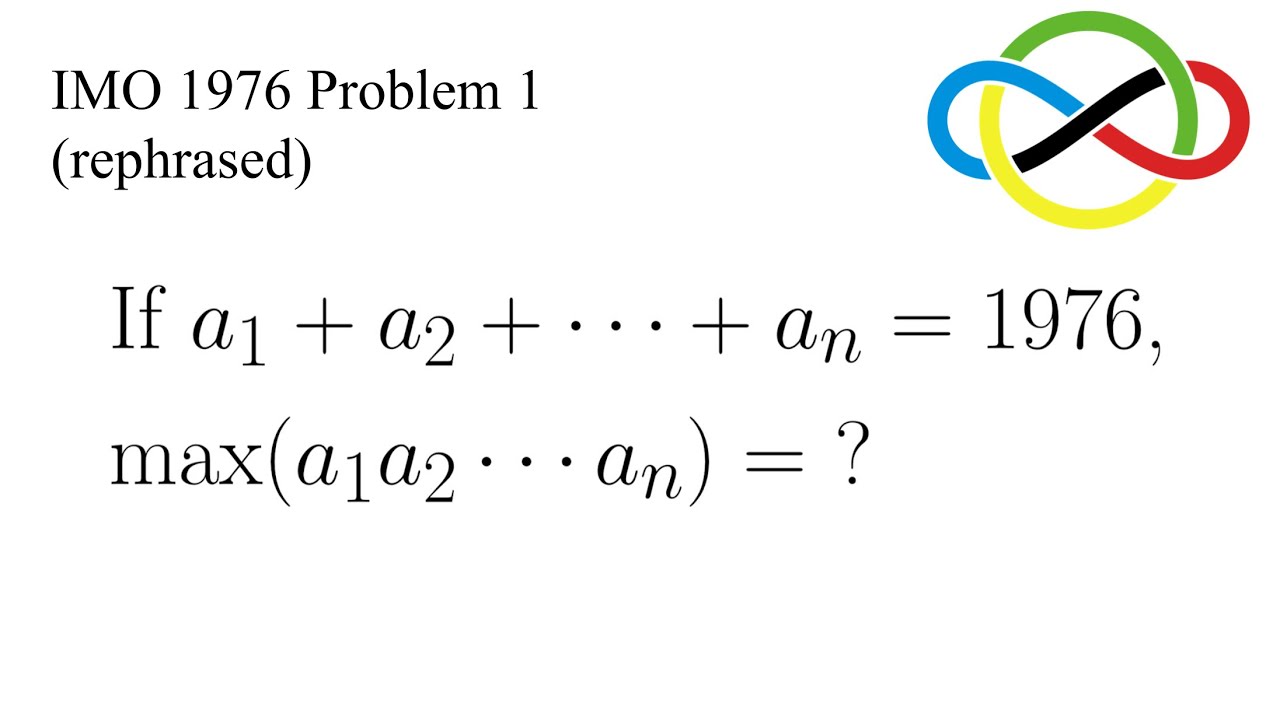
Показать описание
#IMO #Math #MathOlympiad
Here is the solution to IMO 1976 Problem 1!!
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
Follow my Instagram page for more Maths :)
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
Here is the solution to IMO 1976 Problem 1!!
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
Follow my Instagram page for more Maths :)
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
Can Calculus Help Solve IMO Problems? | International Mathematical Olympiad 1976 Problem 4
The unexpectedly hard windmill question (2011 IMO, Q2)
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
How to Prepare for Math Competitions
This U.S. Olympiad Coach Has a Unique Approach to Math
The hardest problem on the hardest test
The Legend of Question Six - Numberphile
Harvard University Entrance Exam | Math Olympiad | Exponential Math | Mathematics | Pi Nerds
Luxembourg - Math Olympiad Question | You should know this trick
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
Terence Tao Teaches Mathematical Thinking | Official Trailer | MasterClass
Solving an IMO Problem in 10 Minutes! | International Mathematical Olympiad 2006 P4
Solving An Insanely Hard Problem For High School Students
Russian l can you solve this exponential problem?? l Olympiad Mathematics
When mathematicians get bored (ep1)
South Korea l can you solve this fractional problem?? l Olympiad Mathematics
You, me, and my first International Math Olympiad problem
MIT Entrance Exam Problem from 1869 #Shorts #math #maths #mathematics #problem #MIT
How REAL Men Integrate Functions
A very interesting polynomial problem that was longlisted for the IMO!
5 simple unsolvable equations
Solving the hardest question of a British Mathematical Olympiad
Mexico - A Nice Math Olympiad Exponential Problem
Комментарии
 0:10:19
0:10:19
 0:16:03
0:16:03
 0:06:40
0:06:40
 0:08:03
0:08:03
 0:03:35
0:03:35
 0:03:20
0:03:20
 0:11:15
0:11:15
 0:08:45
0:08:45
 0:06:14
0:06:14
 0:02:51
0:02:51
 0:00:23
0:00:23
 0:02:10
0:02:10
 0:10:49
0:10:49
 0:07:27
0:07:27
 0:15:12
0:15:12
 0:00:37
0:00:37
 0:11:53
0:11:53
 0:31:21
0:31:21
 0:00:48
0:00:48
 0:00:35
0:00:35
 0:10:10
0:10:10
 0:00:50
0:00:50
 0:11:26
0:11:26
 0:08:36
0:08:36