filmov
tv
A very interesting polynomial problem that was longlisted for the IMO!

Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A very interesting polynomial problem that was longlisted for the IMO!
An Interesting Polynomial System
Polynomial Functions in Our Everyday Lives
Interesting Polynomial Coefficient Problem
How are 67 and 2010 useful for this polynomial problem?
A nice polynomial problem with primes.
An Interesting Polynomial System
A Cool Polynomial Equation | Math Olympiads
Solving An Interesting Polynomial System in Two Ways
An Interesting Polynomial System with Three Variables
How to solve a polynomial inequality?
How to Identify an Algebraic Expression as Polynomial or Not || Identifying Polynomials | Hindi/Urdu
Solving Polynomial Equations By Factoring and Using Synthetic Division
Algebra Basics: What Are Polynomials? - Math Antics
4th degree polynomial equation a=? Easy or Hard depending on your Algebra skills!
Let's Solve A Nice Polynomial Equation | Math Olympiads
Master Algebra with Brainingcamp's Algebra Tiles - Your Visual Shortcut to Polynomial Success!
A Nice Polynomial Equation
A Cool Polynomial Equation | Algebra
2 seconds trick to factorise cubic polynomial #mathtricks #fastcalculation
Interesting Polynomial Question (x³-kx+1=0 with root between x=0 & x=1)
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
Solving Polynomial Equations - Grade 10 Math
Solving A Nice Polynomial System | Algebra
Комментарии
 0:10:10
0:10:10
 0:16:30
0:16:30
 0:01:50
0:01:50
 0:16:16
0:16:16
 0:12:46
0:12:46
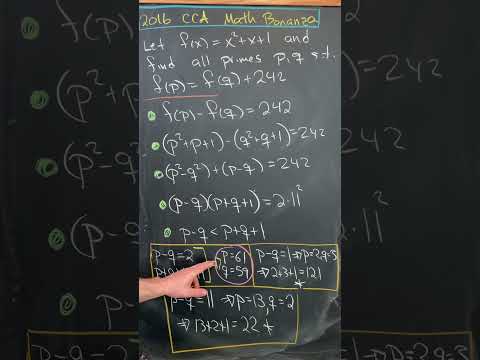 0:01:00
0:01:00
 0:09:58
0:09:58
 0:11:00
0:11:00
 0:12:01
0:12:01
 0:09:25
0:09:25
 0:00:58
0:00:58
 0:11:47
0:11:47
 0:14:19
0:14:19
 0:11:09
0:11:09
 0:19:04
0:19:04
 0:10:49
0:10:49
 0:00:24
0:00:24
 0:00:51
0:00:51
 0:08:47
0:08:47
 0:00:30
0:00:30
 0:05:54
0:05:54
 0:01:01
0:01:01
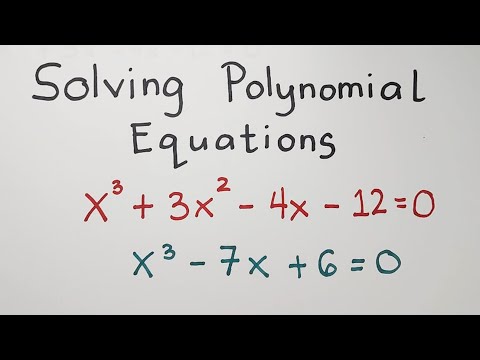 0:12:02
0:12:02
 0:08:57
0:08:57