filmov
tv
Solving an IMO Problem in 10 Minutes! | International Mathematical Olympiad 2006 P4
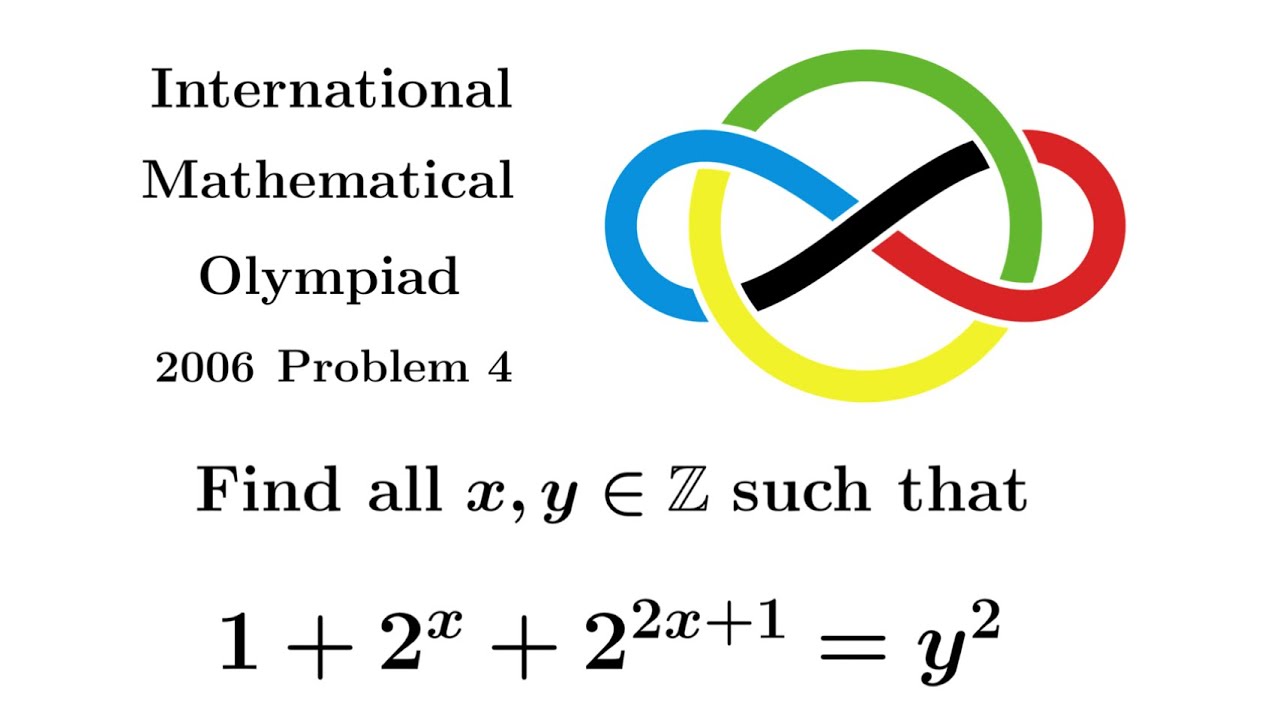
Показать описание
#NumberTheory #MathOlympiad #IMO
The International Mathematical Olympiad is the biggest Mathematics Contest for high school students, with the most number of participating countries. The contest is held over 2 days, when contestants work on 6 problems within a total of 9 hours. Now we are going to smash one of them in 10 minutes!
————————————————————————————————————————————————
I have just launched my Instagram page! Follow for more Maths :)
————————————————————————————————————————————————
I share maths problems and maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
The International Mathematical Olympiad is the biggest Mathematics Contest for high school students, with the most number of participating countries. The contest is held over 2 days, when contestants work on 6 problems within a total of 9 hours. Now we are going to smash one of them in 10 minutes!
————————————————————————————————————————————————
I have just launched my Instagram page! Follow for more Maths :)
————————————————————————————————————————————————
I share maths problems and maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
The unexpectedly hard windmill question (2011 IMO, Q2)
Solving an IMO Problem in 10 Minutes!! | International Mathematical Olympiad 1992 Problem 1
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
Solving an IMO Problem in 10 Minutes! | International Mathematical Olympiad 2006 P4
Solving an IMO Problem in 10 Minutes!! | International Mathematical Olympiad 2019 Problem 1
Olympiad Number Theory for Beginners - HOW to Solve IMO 2023 Problem 1
Solving an IMO Problem in Two Ways in Under 4 Minutes!
2024 IMO Problem 1: Interesting Algebra and Number Theory
Chinese IMO team
IMO 2024 - Problem 1: A cool Algebra with integer parts and bounding :)
Solving IMO 2020 Q2 in 7 Minutes!! | International Mathematical Olympiad 2020 Problem 2
IMO 2024 Problem 5 - most *TROLL* problem in IMO history?
IMO 2024 Problem 1 Trump SOLVE ( it is easy actually)
Almost an IMO Problem | IMO Shortlist 2019 N2
Solving An Insanely Hard Problem For High School Students
You, me, and my first International Math Olympiad problem
IMO 2024 Problem 1 - Neat little problem to start things off!
Solving an IMO problem in 5 minutes: IMO 1962 – Problem 1
imo app fix Cannot call this user due to his/her privacy settings ( Standard SMS rates Problem Solve
A simple solution to a difficult problem - Problem 5 at IMO 2021 (SoME1 submission)
Geometry question to test the world's best math students (IMO 2024 problem 4)
International Math Olympiad, IMO 2023, Problem 1
Trial and Error for an IMO Problem!? | International Mathematical Olympiad 1960 Problem 1
Комментарии
 0:06:40
0:06:40
 0:16:03
0:16:03
 0:10:33
0:10:33
 0:08:03
0:08:03
 0:10:49
0:10:49
 0:12:03
0:12:03
 0:08:33
0:08:33
 0:03:47
0:03:47
 0:04:07
0:04:07
 0:00:34
0:00:34
 0:16:26
0:16:26
 0:07:35
0:07:35
 0:20:41
0:20:41
 0:04:44
0:04:44
 0:09:13
0:09:13
 0:07:27
0:07:27
 0:31:21
0:31:21
 0:09:27
0:09:27
 0:05:25
0:05:25
 0:01:51
0:01:51
 0:10:58
0:10:58
 0:20:28
0:20:28
 0:06:52
0:06:52
 0:12:36
0:12:36