filmov
tv
Abstract Algebra, Lec 10B: Symmetric Group S3, Generators & Relations, Permutation Properties
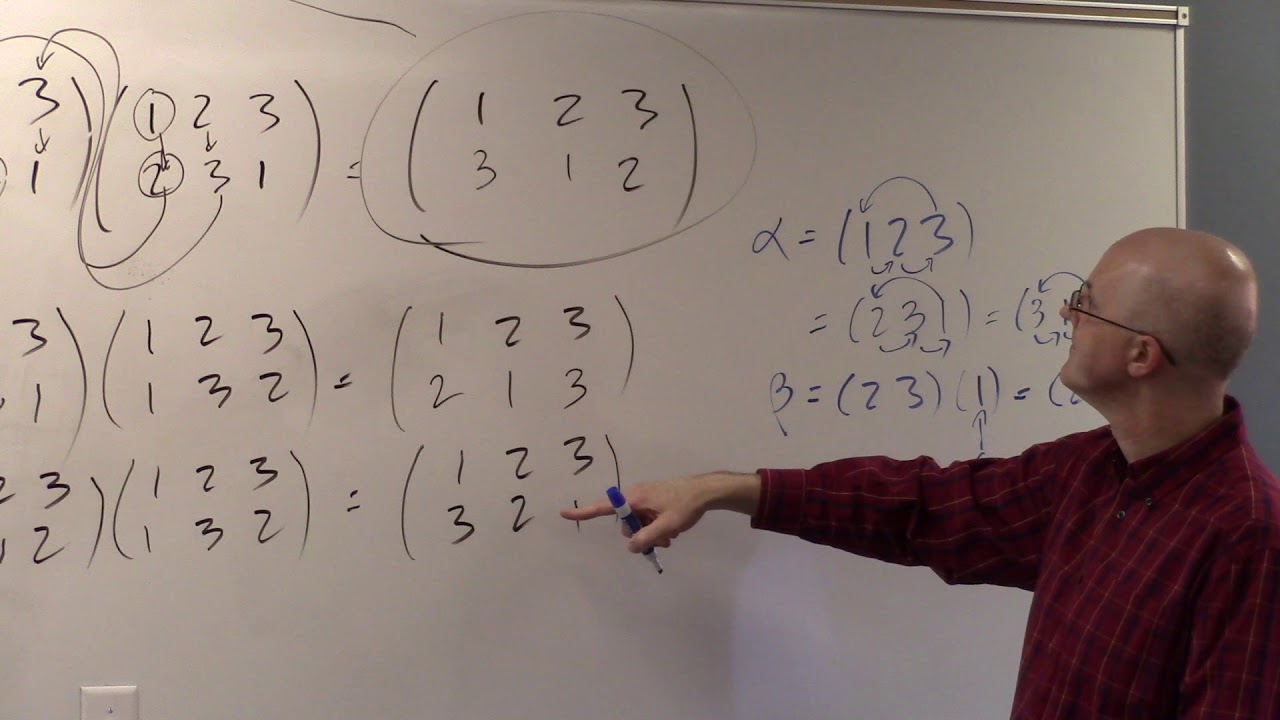
Показать описание
(0:00) Check the claim that S3 can be represented as combinations of a 3-cycle and a 2-cycle (transposition). Use array notation to start with.
(4:46) Cycle notation and composition ("products") of permutations in cycle notation.
(10:32) Generators and relations for S3 and their use to do group computations and create a Cayley table.
(17:44) S3 is isomorphic to D3 (note that alpha and beta could have been chosen differently).
(20:30) Every permutation of a finite set can be written as a cycle or as a product of disjoint cycles.
(22:45) Disjoint cycles commute, but non-disjoint cycles typically do not commute.
(24:31) Order of a permutation of a finite set written in disjoint cycle form (it's the lcm of the lengths of the cycles) and note the fact that Sn is not a subgroup of Sm when n and m are different, though in cycle notation we are free to "think of" a given element as being in some Sn or some Sm of higher degree.
(26:58) Use Mathematica to confirm the order of the example is 12 (it's a composition of disjoint cycles, one of length 3 and the other of length 4, so lcm(3,4) = 12).
(29:16) Permutations as products of two cycles, even & odd permutations, alternating group An of order n!/2.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:31:21
0:31:21
 0:08:02
0:08:02
 0:17:33
0:17:33
 0:08:37
0:08:37
 0:50:29
0:50:29
 0:02:42
0:02:42
 0:30:40
0:30:40
 0:11:07
0:11:07
 0:30:45
0:30:45
 0:02:41
0:02:41
 0:17:00
0:17:00
 0:05:15
0:05:15
 0:36:23
0:36:23
 0:29:56
0:29:56
 0:10:00
0:10:00
 0:05:06
0:05:06
 0:11:42
0:11:42
 0:09:51
0:09:51
 0:25:42
0:25:42
 0:06:17
0:06:17
 0:14:53
0:14:53
 0:35:20
0:35:20
 0:03:35
0:03:35
 0:02:37
0:02:37