B. Hamzi: On Bridging ML, Dynamical Systems, & Algorithmic Info. Th. Via SKFs and PDE Simplification

Title: Bridging Machine Learning, Dynamical Systems, and Algorithmic Information Theory: Insights from Sparse Kernel Flows and PDE Simplification
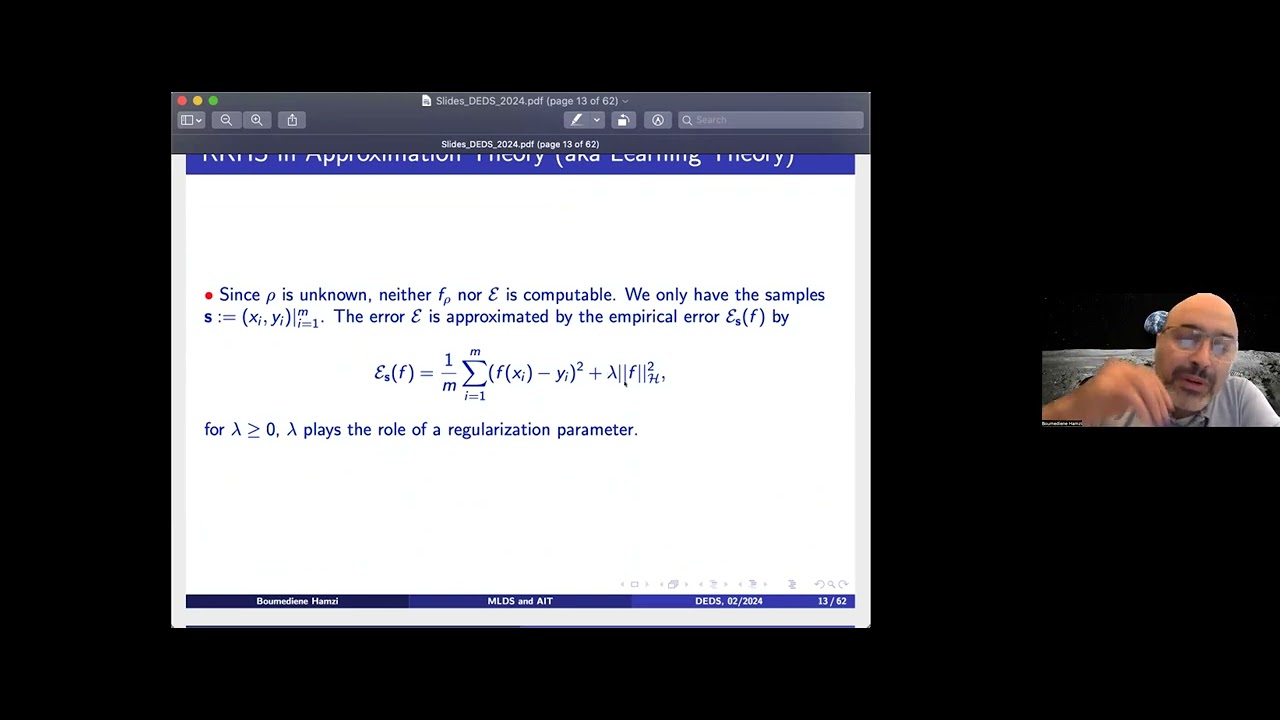
Abstract: This presentation delves into the intersection of Machine Learning, Dynamical Systems, and Algorithmic Information Theory (AIT), exploring the connections between these areas. In the first part, we focus on Machine Learning and the problem of learning kernels from data using Sparse Kernel Flows. We draw parallels between Minimum Description Length (MDL) and Regularization in Machine Learning (RML), showcasing that the method of Sparse Kernel Flows offers a natural approach to kernel learning. By considering code lengths and complexities rooted in AIT, we demonstrate that data-adaptive kernel learning can be achieved through the MDL principle, bypassing the need for cross-validation as a statistical method.
  Transitioning to the second part of the presentation, we shift our attention to the task of simplifying Partial Differential Equations (PDEs) using kernel methods. Here, we utilize kernel methods to learn the Cole-Hopf transformation, transforming the Burgers equation into the heat equation. We argue that PDE simplification can also be seen as an MDL and a compression problem, aiming to make complex PDEs more tractable for analysis and solution. While these two segments may initially seem distinct, they collectively exemplify the multifaceted nature of research at the intersection of Machine Learning, Dynamical Systems, and AIT, offering preliminary insights into the synergies that arise when these fields converge.