filmov
tv
Gaussian Primes Visually

Показать описание
Gaussian Primes Visually
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
Eisenstein Primes Visually #SoMEpi
Constructing Gaussian primes
Gaussian primes
Euclid's Perfects and Mersenne's Primes (visually)
Gaussian Primes part I
Pi hiding in prime regularities
RNT2.4. Gaussian Primes
The Pattern to Prime Numbers?
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Every Student Should See This
Complex Quadratic Integers and Primes
Gaussian Primes in Narrow Sectors, Joshua Stucky
Gaussian integer
This completely changed the way I see numbers | Modular Arithmetic Visually Explained
What is the Riemann Hypothesis REALLY about?
Complex Numbers, Gaussian Integers, Gaussian Rationals, and Euler's Formula
Sieve Of Eratosthenes (visualized)
When mathematicians get bored (ep1)
Gaussian Integers tiling a circle
Imaginary Numbers Are Real [Part 1: Introduction]
How REAL Men Integrate Functions
The HARDEST part about programming 🤦♂️ #code #programming #technology #tech #software #developer...
Комментарии
 0:12:29
0:12:29
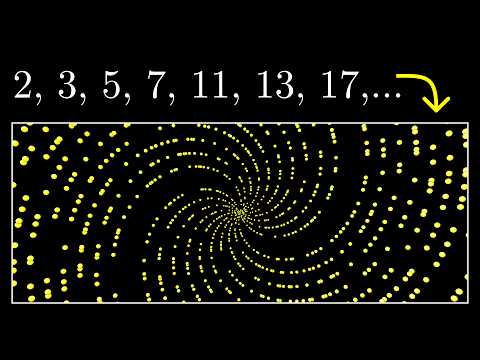 0:22:21
0:22:21
 0:21:45
0:21:45
 0:01:36
0:01:36
 0:11:56
0:11:56
 0:03:43
0:03:43
 0:03:47
0:03:47
 0:30:42
0:30:42
 0:22:31
0:22:31
 0:16:27
0:16:27
 0:00:38
0:00:38
 0:00:58
0:00:58
 0:23:00
0:23:00
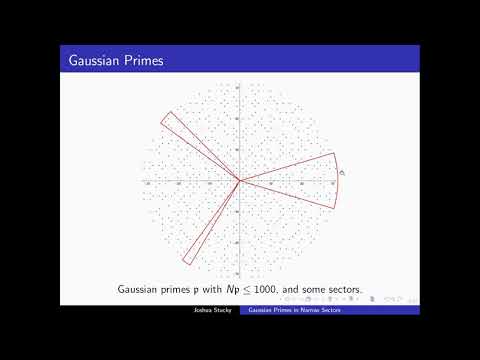 0:23:17
0:23:17
 0:06:25
0:06:25
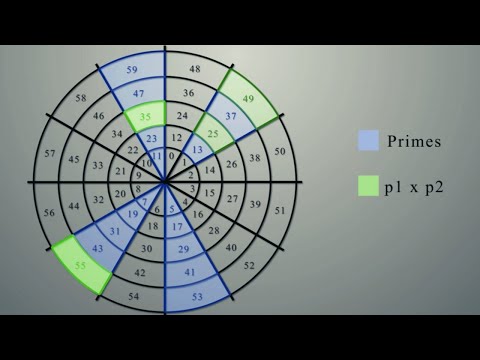 0:20:33
0:20:33
 0:28:33
0:28:33
 0:14:35
0:14:35
 0:01:58
0:01:58
 0:00:37
0:00:37
 0:00:58
0:00:58
 0:05:47
0:05:47
 0:00:35
0:00:35
 0:00:28
0:00:28