Gaussian Primes in Narrow Sectors, Joshua Stucky

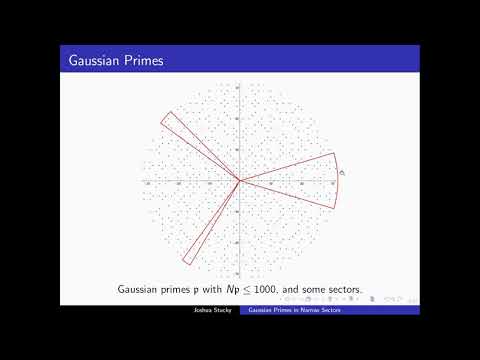
Abstract: Consider a sector in the complex plane which is the region between two concentric circles centered at the origin and which is cut by two rays emanating from the origin. Such a sector is "narrow" if the distance between the circles and/or the angle between the rays is small. Similar to how one investigates the distribution of rational primes in short intervals, we can investigate the distribution of prime ideals in Z[i] in narrow sectors. In this work, we show how one can adapt Heath-Brown's method for counting rational primes in short intervals to obtain an asymptotic count for the number of Gaussian primes in narrow
sectors.

Subject codes: 11N05, 11N25, 11N32