filmov
tv
Solving Linear Systems Using Row Reduction

Показать описание
0:00 Introduction
00:17 Review
00:38 Definition of Basic Variables & Free Variables
00:51 Example - Determine Basic & Free Variables
1:54 Finding Pivot Positions from an Echelon Matrix
Existence and Uniqueness Theorem (E&U Theorem):
3:53 Existence part of E&U Theorem
4:40 Uniqueness part of E&U Theorem
4:53 Example 1 (Echelon Form of a Consistent System with Infinitely Many Solutions)
5:23 Example 2 (Echelon Form of an Inconsistent System)
5:38 Example 3 (Echelon Form of a Consistent System with Unique Solution)
6:36 Example - Solve the linear system by finding the reduced echelon form
8:01 Example continued - A parametric description of the solution set with the free variables as parameters
9:31 Example continued - A different parametric description of the solution set.
10:12 General Procedure for Solving Linear Systems Using Row Reduction
11:03 Video Summary
Review:
- The leading entry of a nonzero row is the leftmost nonzero entry of the row.
- An echelon form of a matrix A is an echelon matrix that is row equivalent to A. (For any matrix A, there are infinitely many echelon forms of A).
- A reduced echelon form of a matrix A is a reduced echelon matrix that is row equivalent to A. (For any matrix A, there is exactly one reduced echelon form of A).
- A pivot position in a matrix A is a location in A corresponding to a leading 1 in the reduced echelon form of A. A pivot column of A is a column of A that contains a pivot position.
New Material:
- An unknown variable of a linear system S is called a basic variable if it corresponds to a pivot column in the augmented matrix of S. Otherwise, the variable is called a free variable.
- (Number of nonzero rows in an echelon matrix) = (Number of pivot columns) = (Number of basic variables in corresponding system)
- Existence & Uniqueness Theorem:
A linear system is consistent if and only if the rightmost column of the augmented matrix is not a linear system. That is, if and only if an echelon form of the augmented matrix has no row of the form [ 0 . . . 0 | b ], with b nonzero.
If a linear system is consistent, then the solution set contains either
(a) A unique solution, when there are no free variables
(b) Infinitely many solutions, when there is at least one free variable
00:17 Review
00:38 Definition of Basic Variables & Free Variables
00:51 Example - Determine Basic & Free Variables
1:54 Finding Pivot Positions from an Echelon Matrix
Existence and Uniqueness Theorem (E&U Theorem):
3:53 Existence part of E&U Theorem
4:40 Uniqueness part of E&U Theorem
4:53 Example 1 (Echelon Form of a Consistent System with Infinitely Many Solutions)
5:23 Example 2 (Echelon Form of an Inconsistent System)
5:38 Example 3 (Echelon Form of a Consistent System with Unique Solution)
6:36 Example - Solve the linear system by finding the reduced echelon form
8:01 Example continued - A parametric description of the solution set with the free variables as parameters
9:31 Example continued - A different parametric description of the solution set.
10:12 General Procedure for Solving Linear Systems Using Row Reduction
11:03 Video Summary
Review:
- The leading entry of a nonzero row is the leftmost nonzero entry of the row.
- An echelon form of a matrix A is an echelon matrix that is row equivalent to A. (For any matrix A, there are infinitely many echelon forms of A).
- A reduced echelon form of a matrix A is a reduced echelon matrix that is row equivalent to A. (For any matrix A, there is exactly one reduced echelon form of A).
- A pivot position in a matrix A is a location in A corresponding to a leading 1 in the reduced echelon form of A. A pivot column of A is a column of A that contains a pivot position.
New Material:
- An unknown variable of a linear system S is called a basic variable if it corresponds to a pivot column in the augmented matrix of S. Otherwise, the variable is called a free variable.
- (Number of nonzero rows in an echelon matrix) = (Number of pivot columns) = (Number of basic variables in corresponding system)
- Existence & Uniqueness Theorem:
A linear system is consistent if and only if the rightmost column of the augmented matrix is not a linear system. That is, if and only if an echelon form of the augmented matrix has no row of the form [ 0 . . . 0 | b ], with b nonzero.
If a linear system is consistent, then the solution set contains either
(a) A unique solution, when there are no free variables
(b) Infinitely many solutions, when there is at least one free variable
 0:07:18
0:07:18
 0:07:27
0:07:27
 0:18:40
0:18:40
 0:08:48
0:08:48
 0:27:47
0:27:47
 0:10:51
0:10:51
 0:23:35
0:23:35
 0:10:36
0:10:36
 0:51:19
0:51:19
 0:16:25
0:16:25
 0:18:04
0:18:04
 0:12:10
0:12:10
 0:05:06
0:05:06
 0:11:11
0:11:11
 0:06:39
0:06:39
 0:09:42
0:09:42
 0:15:44
0:15:44
 0:08:23
0:08:23
 0:04:53
0:04:53
 0:10:17
0:10:17
 0:11:03
0:11:03
 0:02:08
0:02:08
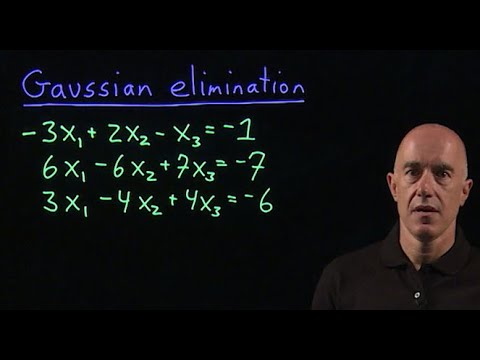 0:14:00
0:14:00
 0:07:18
0:07:18