filmov
tv
Linear Algebra 1.1.2 Solve Systems of Linear Equations in Augmented Matrices Using Row Operations

Показать описание
Linear Algebra 1.1.2 Solve Systems of Linear Equations in Augmented Matrices Using Row Operations
Linear Algebra - 27 - Algebraic Systems of Equations with Matrices
How do we solve a system of linear equations using any method
Gaussian Elimination & Row Echelon Form
Linear Algebra 1.1.1 Systems of Linear Equations
Algebra - Solving Linear Equations by using the Graphing Method 1/2
Solving Systems of Equations By Elimination & Substitution With 2 Variables
Solving Systems of Equations By Graphing
CAT 2024 Quantitative Aptitude | 250+ Must-Do Quant Questions - 15
Algebra - Solving Linear Equations by Inverse Matrix Method 1/2
Linear Algebra 1.2.2 Solution Sets and Free Variables
Linear Algebra - Matrix Operations
Vectors | Chapter 1, Essence of linear algebra
[Linear Algebra] Solving Systems of Equations
Gauss Jordan Elimination & Reduced Row Echelon Form
Linear Equations - Algebra
Intro to Matrices
A unique solution, No solution, or Infinitely many solutions | Ax=b
Solving Matrix Equations
Method of Elimination Steps to Solve Simultaneous Equations
Using Elimination to Solve Systems
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
How To Solve Linear Inequalities, Basic Introduction, Algebra
Solving Systems of Equations... Elimination Method (NancyPi)
Комментарии
 0:07:18
0:07:18
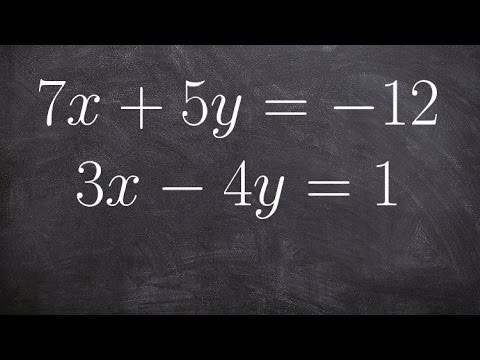 0:04:34
0:04:34
 0:18:40
0:18:40
 0:18:18
0:18:18
 0:05:06
0:05:06
 0:10:27
0:10:27
 0:05:15
0:05:15
 0:54:05
0:54:05
 0:09:42
0:09:42
 0:14:19
0:14:19
 0:07:08
0:07:08
 0:09:52
0:09:52
![[Linear Algebra] Solving](https://i.ytimg.com/vi/hk0gn0JgYGY/hqdefault.jpg) 0:15:05
0:15:05
 0:10:51
0:10:51
 0:32:05
0:32:05
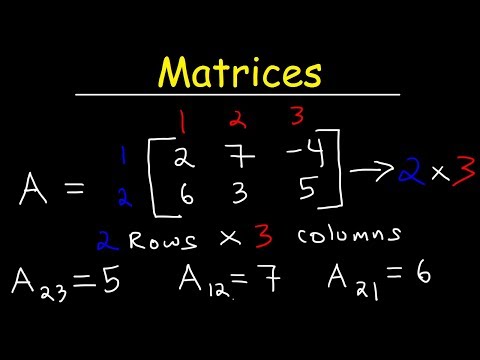 0:11:23
0:11:23
 0:13:08
0:13:08
 0:06:31
0:06:31
 0:02:58
0:02:58
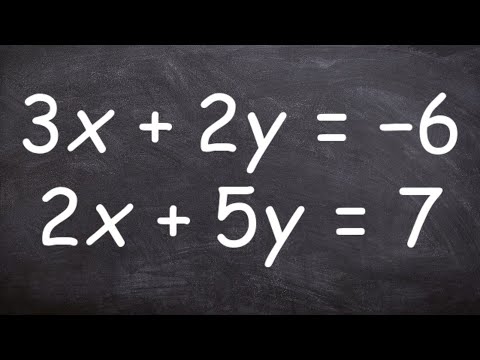 0:09:22
0:09:22
 0:10:21
0:10:21
 0:06:24
0:06:24
 0:19:44
0:19:44