filmov
tv
tricky calculus limits you need to be careful!

Показать описание
We will discuss the limit of sin(ln(x))/x x goes to 0+ vs. the limit of sin(ln(x))/x as x goes to inf. These two limits are suitable for precalculus and calculus 1 students.
tricky calculus limits you need to be careful!
Calculus 1 - Introduction to Limits
100 calculus limits (ft epsilon-delta definition and Riemann sum limits )
A tricky derivative using the limit definition #calculus
How to Make it Through Calculus (Neil deGrasse Tyson)
Baby calculus vs adult calculus
Calculus in a nutshell
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Calculus 2: Solving Exam 3 -All things SEQUENCES & SERIES! -Fall 2019 Part 1| Math with Profess...
Introduction to limits | Limits | Differential Calculus | Khan Academy
Calculus, But NO Calculators...
Why People FAIL Calculus (Fix These 3 Things to Pass)
A 'cruel' limit for a beginning calculus class
3 calculus questions to make you feel good
Every Student Should See This
Limits That Approach Infinity (Calculus)
What Makes Calculus Hard #shorts
Calculus Students HATE This Problem!!
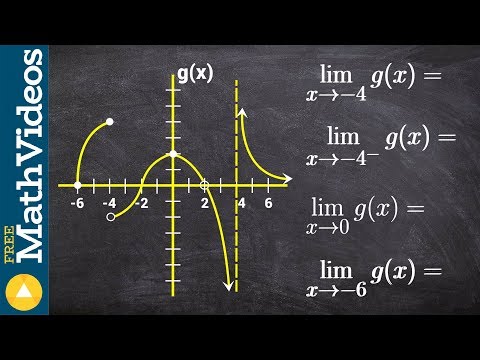
Evaluate all the limits from a given graph
How To VISUALIZE Calculus!!
A COUNTER-INTUITIVE CALCULUS LIMIT
What is the Hardest Calculus Course?
Calculus can be tough...
when calculus students use trig identities too early
Комментарии
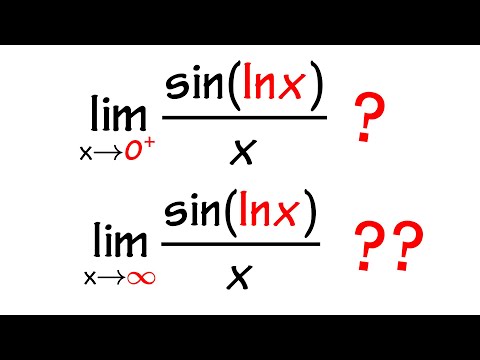 0:06:26
0:06:26
 0:20:20
0:20:20
 7:29:13
7:29:13
 0:00:38
0:00:38
 0:03:38
0:03:38
 0:00:27
0:00:27
 0:03:01
0:03:01
 0:00:09
0:00:09
 1:05:21
1:05:21
 0:11:32
0:11:32
 0:01:00
0:01:00
 0:03:15
0:03:15
 0:10:05
0:10:05
 0:00:46
0:00:46
 0:00:58
0:00:58
 0:00:59
0:00:59
 0:00:29
0:00:29
 0:00:59
0:00:59
 0:05:34
0:05:34
 0:01:00
0:01:00
 0:11:30
0:11:30
 0:01:44
0:01:44
 0:00:58
0:00:58
 0:00:43
0:00:43