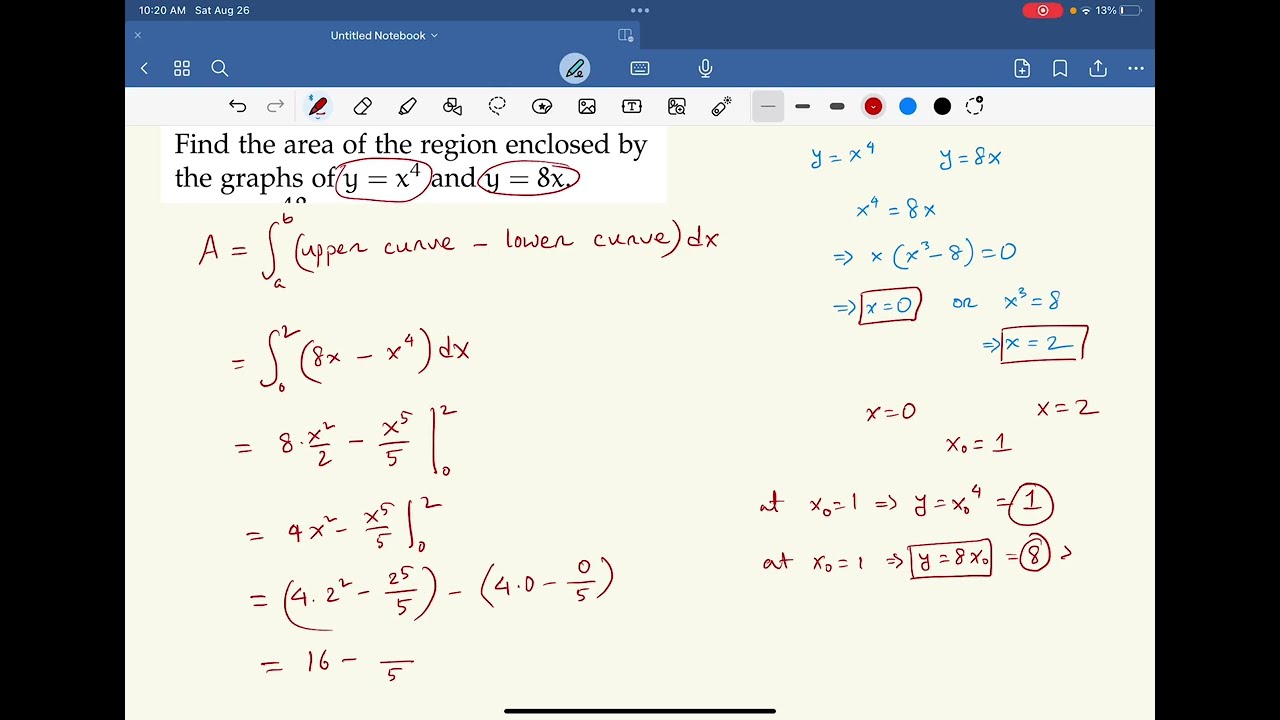
Find the area of the region enclosed by the graphs: y = x^4 and y = 8x

📐 Exploring Calculus: Finding the Area Enclosed by Curves 📐

Welcome to our latest math adventure! 🎉 In this exciting YouTube video, we delve into the world of calculus to tackle a fascinating problem: finding the area of the region enclosed by the graphs of two curves, y = x^4 and y = 8x.

🔍 Curious minds, get ready to:

📌 **Understand Curve Intersection:** We kick off by analyzing the points of intersection between the curves y = x^4 and y = 8x. Exploring these points opens the door to calculating the limits of integration.

📌 **Setting Up the Integral:** Learn step-by-step how to set up the definite integral that represents the area of the enclosed region. We'll walk you through the process of choosing the proper bounds and integrands to capture the entire area accurately.

📌 **Integration Techniques:** Dive into the world of integration as we guide you through the techniques required to solve the definite integral. Whether it's using the power rule or applying substitution, you'll gain valuable insights into solving real-world problems with calculus.

Get ready to exercise your brain cells and embrace the beauty of mathematical problem-solving! Whether you're a student brushing up on your calculus skills or simply someone who loves exploring the intricacies of mathematics, this video is tailored for you.

🔗 Don't forget to like, comment, and subscribe to our channel to stay updated with more captivating math content. Hit the notification bell so you never miss out on our explorations into the world of numbers, functions, and equations. Let's unlock the secrets of calculus together!

📢 Put your questions and concerns in the comments. Happy calculating! 🧮🤓