filmov
tv
Solving a Quadratic Diophantine Equation
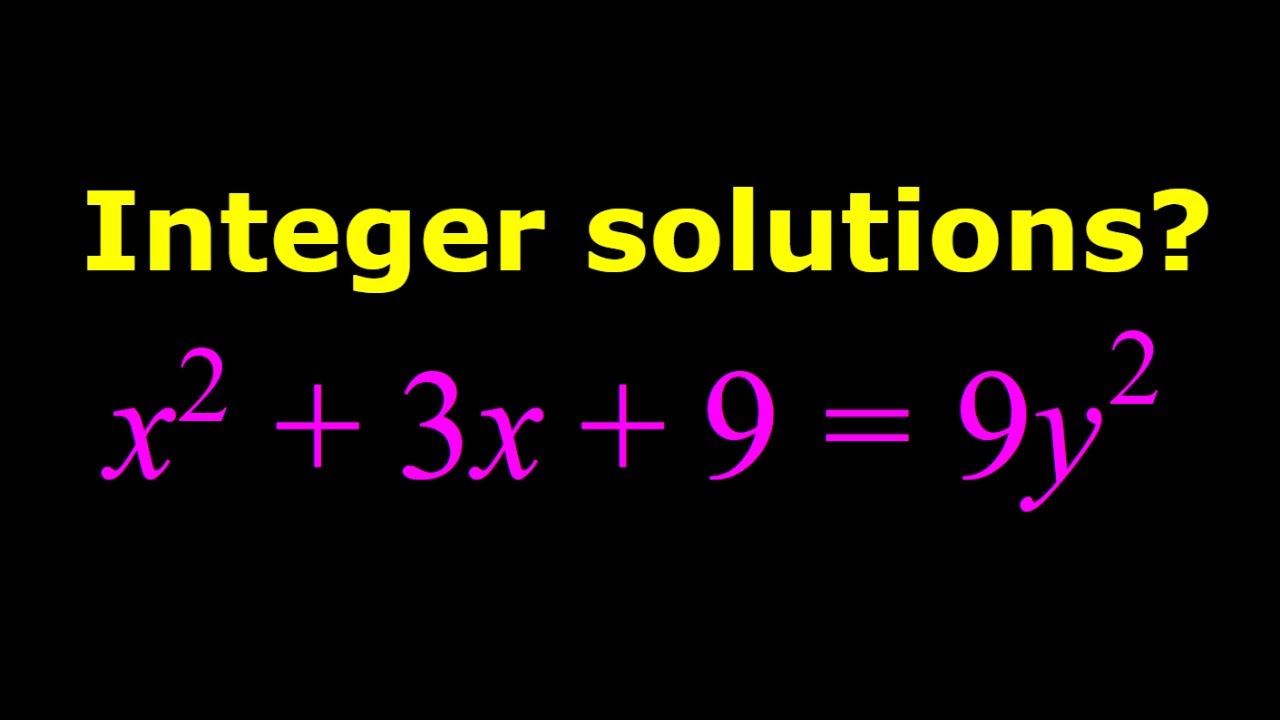
Показать описание
This video is about a quadratic diophantine equation.
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #DiophantineEquations
2 BOOKS and SOME LINKS:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #DiophantineEquations
2 BOOKS and SOME LINKS:
Solving a Quadratic Diophantine Equation
Solving a Quadratic Diophantine Equation
A Quadratic Diophantine Equation | Math Olympiads
I Solved A Quadratic Diophantine Equation | Integer Solutions?
Cool Algebraic Tricks! | How to Solve the Quadratic Diophantine Equation?
Quadratic Diophantine Equations with One Variable
Quadratic Diophantine Equations with Two Variables
Solving a quadratic Diophantine equation w CS method!
Factoring in a Quadratic Diophantine Equation || High School Math
A Quick and Easy Diophantine Equation
Solve Diophantine Equations by Factoring
Quadratic Diophantine Contradicitions
Number Theory | A few nonlinear Diophantine equations without solutions.
Diophantine Equations: Strategies and Examples
A Tough Diophantine Equation!
A Diophantine Equation @drpkmath1234
Solving The Diophantine Equation x^2+y^2=z^4
A USAMO Problem: Solve Diophantine Equation (Easier Than You Think)
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
How to Solve Quadratic Diophantine Equation | ISI BStat BMath Entrance 2015 Obj 12 | Math Olympiad
Solve Diophantine Equation by Factoring
Solving A Cool Diophantine Equation With Integers
I Solved A Diophantine Equation in Three Ways
A Linear Diophantine Equation
Комментарии
 0:11:04
0:11:04
 0:11:04
0:11:04
 0:10:19
0:10:19
 0:10:40
0:10:40
 0:03:29
0:03:29
 0:04:04
0:04:04
 0:04:07
0:04:07
 0:10:50
0:10:50
 0:07:44
0:07:44
 0:05:37
0:05:37
 0:01:58
0:01:58
 0:05:13
0:05:13
 0:04:09
0:04:09
 0:27:34
0:27:34
 0:09:52
0:09:52
 0:14:11
0:14:11
 0:08:40
0:08:40
 0:00:59
0:00:59
 0:07:08
0:07:08
 0:07:16
0:07:16
 0:00:35
0:00:35
 0:10:57
0:10:57
 0:10:23
0:10:23
 0:00:27
0:00:27