Solving A Cool Diophantine Equation With Integers

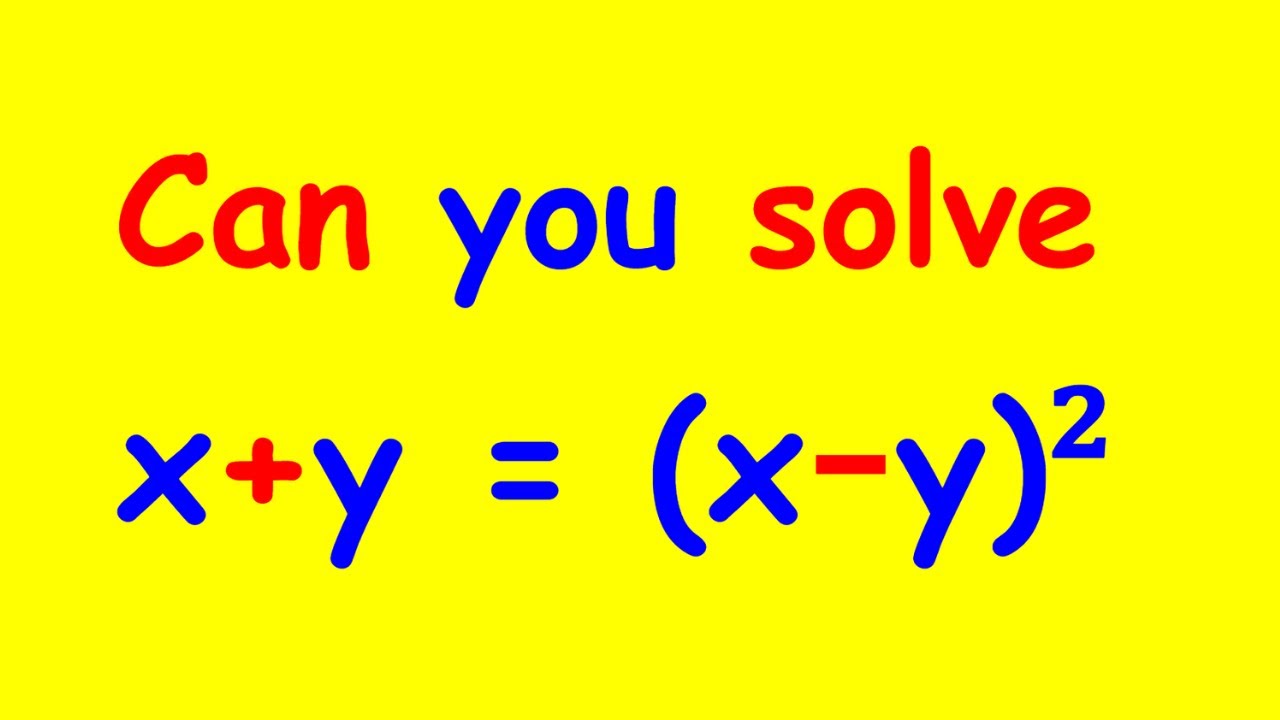
preview_player
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡

If you need to post a picture of your solution or idea:
#numbertheory #diophantineequations #integers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :
  1. SyberMath Shorts
Рекомендации по теме
Solving A Cool 0:10:57

Solving A Cool Diophantine Equation With Integers

A Nice Diophantine 0:07:40

A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad

Diophantine Equation: ax+by=gcd(a,b) 0:09:43

Diophantine Equation: ax+by=gcd(a,b) ← Number Theory

Solving a Cool 0:05:17

Solving a Cool Diophantine Equation: a^2+a+34=b^2

A Cool Diophantine 0:04:36

A Cool Diophantine Equation

Let's Solve A 0:07:34

Let's Solve A Cool Diophantine Equation

Diophantine Equations: Strategies 0:27:34

Diophantine Equations: Strategies and Examples

Solving a Cool 0:03:23

Solving a Cool Diophantine Problem | Solve For Integer Values

Number Theory | 0:09:17

Number Theory | Linear Diophantine Equations

Solve Diophantine Equations 0:01:58

Solve Diophantine Equations by Factoring

A Linear Diophantine 0:00:27

A Linear Diophantine Equation

Cool Algebraic Tricks! 0:03:29

Cool Algebraic Tricks! | How to Solve the Quadratic Diophantine Equation?

Solving A Set 0:00:58

Solving A Set Of Diophantine Equation In Under A Minute

Solving a Diophantine 0:07:08

Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory

Cool Trick for 0:03:51

Cool Trick for Solving the Diophantine Equation (x+y)^2=x^3+y^3 | Integer Solution | Math Olympiad

Solving a Quadratic 0:11:04

Solving a Quadratic Diophantine Equation

How To Solve 0:10:24

How To Solve Linear Diophantine Equations

Solving A Diophantine 0:00:54

Solving A Diophantine Equation with Prime Numbers

A Diophantine Equation 0:00:55

A Diophantine Equation | x^2-y^2=23

Cool Tricks! | 0:06:15

Cool Tricks! | Solving the Challenging Diophantine Equation a^2+ab+b^2=343 | Math Olympiad

A Diophantine Equation 0:00:49

A Diophantine Equation with Integer Solutions

A Nice Diophantine 0:08:57

A Nice Diophantine Equation

A Diophantine Equation 0:00:46

A Diophantine Equation | a^2=b^2+13

A Cool Diophantine 0:07:09

A Cool Diophantine Equation

Комментарии
Автор

The unsaid fact: n(n+1)/2 is the nth triangular number. Also, any time 8n+1 (where n is any variable or expression representing an integer) turns up alone under a square root, you can be sure that triangular numbers are lurking somewhere. A bit like if n^2-n-1 shows up then there's usually a golden ratio afoot.

lagomoof
Автор

If x + y = k^2 then x - y can be k or (-k). Hence the 2 solutions you got with the 1st method.

FisicTrapella
Автор

took me a while of bashing my skull in to the wall with congruence, parity, perfect squares and divisibility, but then the solution hit me and i felt kind of dumb..

Set x-y=n, therefore x=y+n
Replace in our original equation to get n+y+y=n^2
Cleaning up you get y = ½(n^2 - n)
Do the same for y=x-n, x= ½(n^2 + n)
The solution set to our original equation is (x, y) = [½(n^2 + n), ½(n^2 - n)] for every integer n

barberickarc
Автор

For the 2nd method, to avoid invalid solution value w/o checking, note that
x+y=(x-y)² --> x+y is positive
It means that
• both x and y can't be negative
• both x and y are positive or
• one of x and y is positive and the other one is negative but the absolute value of the negative one is less than the positive. To be clearer, let say y<0. Then |y|<x. Hope tham I'm right.

nasrullahhusnan