filmov
tv
I Solved A Quadratic Diophantine Equation | Integer Solutions?

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #diophantineequations #numbertheoryproblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #diophantineequations #numbertheoryproblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
I Solved A Quadratic Diophantine Equation | Integer Solutions?
Solving a Quadratic Diophantine Equation
Solving a Quadratic Diophantine Equation
A Quadratic Diophantine Equation | Math Olympiads
Factoring in a Quadratic Diophantine Equation || High School Math
Cool Algebraic Tricks! | How to Solve the Quadratic Diophantine Equation?
Quadratic Diophantine Contradicitions
I Solved A Diophantine Equation in Three Ways
5 simple unsolvable equations
Solve Diophantine Equations by Factoring
A Diophantine Equation with Integer Solutions
Solving a quadratic Diophantine equation w CS method!
Quadratic Diophantine Equations with One Variable
I Solved A Diophantine Equation
2023 Number Challenge: Solve the Diophantine Equation, leave your answer in the comments
Quadratic Equations IIT Questions No 11 ( X Class)
I Solved An Interesting Diophantine Equation
Solve Diophantine Equation by Factoring
The disappointing solutions to a nonlinear Diophantine equation
A USAMO Problem: Solve Diophantine Equation (Easier Than You Think)
I Solved A Diophantine Equation from Moscow #integers
When mathematicians get bored (ep1)
Quadratic Diophantine equation - Polynomial Time Cases
A Quadratic Diophantine Equation | Collab with @drpkmath1234
Комментарии
 0:10:40
0:10:40
 0:11:04
0:11:04
 0:11:04
0:11:04
 0:10:19
0:10:19
 0:07:44
0:07:44
 0:03:29
0:03:29
 0:05:13
0:05:13
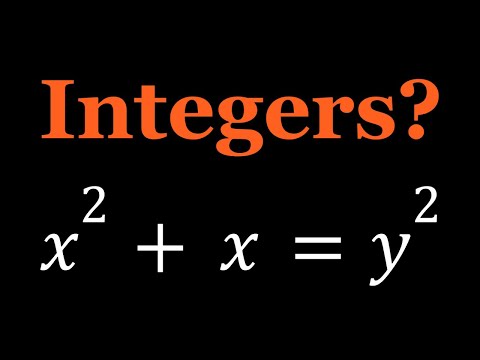 0:10:23
0:10:23
 0:00:50
0:00:50
 0:01:58
0:01:58
 0:00:49
0:00:49
 0:10:50
0:10:50
 0:04:04
0:04:04
 0:07:41
0:07:41
 0:00:56
0:00:56
 0:00:50
0:00:50
 0:05:28
0:05:28
 0:00:35
0:00:35
 0:00:37
0:00:37
 0:00:59
0:00:59
 0:09:04
0:09:04
 0:00:37
0:00:37
 0:01:36
0:01:36
 0:10:52
0:10:52