filmov
tv
Solving an Interesting Diophantine Equation in Number Theory - Math Olympiad

Показать описание
In this video, I am presenting step-by-step solution to this interesting diophantine equation. After a few steps, we come up with a surprisingly easy solution to this diophantine equation. This video contains very important skills to perform when solving a diophantine equation, and it will help you solve more complicated diophantine equation. This question will also be a good problem for math olympiad if you prepare one. Come check this question and watch it until the end. You will get a skill to be used for almost any type of diophantine equation. More to come! Stay tuned!
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #diophantineequation #matholympiad
💬 Did you enjoy this video? Tell me all about it in the comment section below!
Subscribe to Dr. PK Math here ⤵️
*************
✅ Follow Modern Dr PK Math on social media:
*************
#DrPKMath #diophantineequation #matholympiad
Solving an Interesting Diophantine Equation in Number Theory - Math Olympiad
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
I Solved An Interesting Diophantine Equation
Diophantine Equations: Strategies and Examples
Solve Diophantine Equations by Factoring
A Surprisingly Interesting Diophantine Equation in Number Theory | Math Olympiad
Number Theory | Linear Diophantine Equations
Solving A Cool Diophantine Equation With Integers
How To Solve An Interesting Diophantine Equation
A Nice Diophantine Equation from Russian Math Olympiad with Interesting Skills You Should Know
An Interesting Diophantine Equation | Math Olympiad
Solving a Cool Diophantine Equation: a^2+a+34=b^2
A Surprisingly Easy Exponential Diophantine Equation to Solve in Algebra - Math Olympiad
A Linear Diophantine Equation
Solving a Diophantine Equation From USA | y^3-2x^2=1388 Solve For Integer Solutions | Math Olympiad
A Diophantine Equation | x^2-y^2=23
An Interesting Diophantine Equation in Number Theory - You Should Learn This Trick
Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory
An Interesting Diophantine Equation in Number Theory with @PrimeNewtons
A Diophantine Equation with Integer Solutions
5 simple unsolvable equations
A Cool Diophantine Equation
Solving A Set Of Diophantine Equation In Under A Minute
Комментарии
 0:07:35
0:07:35
 0:07:40
0:07:40
 0:09:43
0:09:43
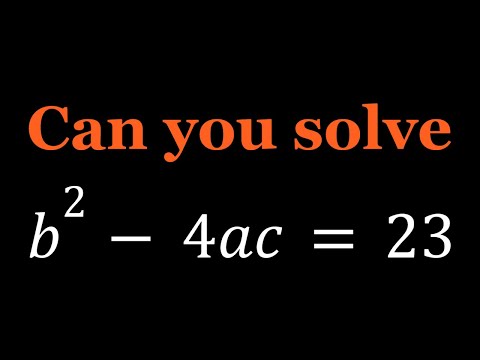 0:05:28
0:05:28
 0:27:34
0:27:34
 0:01:58
0:01:58
 0:06:36
0:06:36
 0:09:17
0:09:17
 0:10:57
0:10:57
 0:09:31
0:09:31
 0:08:26
0:08:26
 0:12:24
0:12:24
 0:05:17
0:05:17
 0:05:54
0:05:54
 0:00:27
0:00:27
 0:04:40
0:04:40
 0:00:55
0:00:55
 0:07:27
0:07:27
 0:07:08
0:07:08
 0:07:32
0:07:32
 0:00:49
0:00:49
 0:00:50
0:00:50
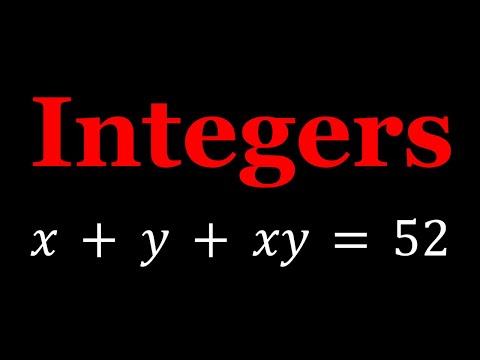 0:04:36
0:04:36
 0:00:58
0:00:58