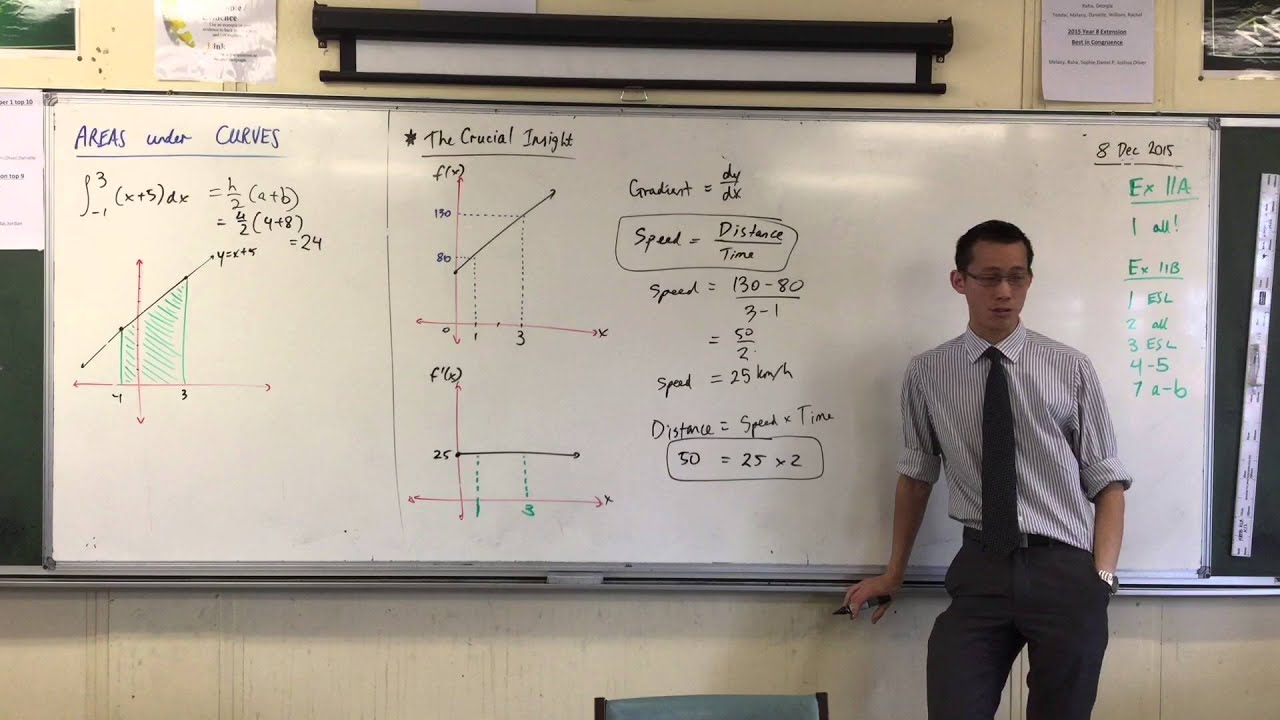
Area under Curves (Continued) (1 of 2: Relationship between Differentiation and Integration)

Показать описание

Рекомендации по теме

Комментарии

7 years on and still helping thousands of us. Thank you so much, this video did it for me.

myrakhoo

The way he approaches the Fundamental Theorem of Calculus is fascinating.

poornakumarage

Wonderful way of expressing the FTC. Brilliant.

boredomgotmehere

Mr Woo thank you for your absolutely flawless way of teaching! I would've never understood the Fundamental Theorem of Calculus without your help!

aries

Mr. Woo is just the best! Thank you very much Sir. You've been of soo much help in my understanding of mathematics

sir-lordwiafe

thank you. this is so helpful. we were just told to use integration to find the area under the curve, it's great to get an explanation of why it works.

calumyoung

Your explanation is amazing. Sometimes I watch your videos to understand physics. Thank you so much :)

ishravlogs

Beautiful introduction of integration.

jayseshidane

thank you so much, this really helps!

blakeparker

Very nice video. So, since (dy)/(dx) = f(x), is it safe to say that integration is just a rearrangement; dy = f(x)(dx) where the sum of f(x)dx over the interval [a, b] is equal to delta F(x) over that same interval?

zacharyf

Area under Curves (Continued) (1 of 2: Relationship between Differentiation and Integration)

Area under Curves (Continued) (1 of 2: Relationship between Differentiation and Integration)

Calculus 1 Lecture 5.1: Finding Area Between Two Curves

Finding the Area Between Two Curves by Integration

What is Integration? Finding the Area Under a Curve

The Story of Integration (1 of 4): Areas Under Curves

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus

Areas under Curves (1 of 4: Using Rectangles with variable widths to estimate area under curves)

Calculus: Areas Between Curves (Section 6.1) | Math with Professor V

Integral of arcsin(x) with Integration by Parts | Calculus 2 Exercises

Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy

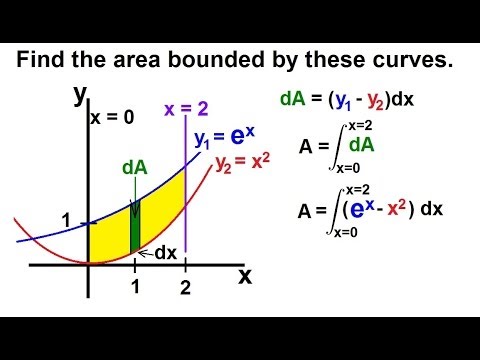
Calculus 2 - Integration: Finding the Area Between Curves (1 of 22) Ex. 1: y=e^x, y=x^2, x=0, x=2

Area under a Curve - Trapezium Rule

Calculus 1 Lecture 4.3: Area Under a Curve, Limit Approach, Riemann Sums

Definite Integral

Finding Areas between Two Curves | Areas of Plane Regions Using Definite Integrals | Calculus

Integration (Calculus)

Properties of Integrals and Evaluating Definite Integrals

Calculus 1 - Integration & Antiderivatives

All of Integration in 30 minutes!!! | Chapter 13 | A Level Pure Maths

Finding the equation of a curve from its gradient function | Tutorial 1 | ExamSolutions

Find the area enclosed by the two curves

Area Under Velocity Time Graphs | Forces & Motion | Physics | FuseSchool

Integration : Parametric type (Area under a graph) : ExamSolutions

#1. How to plot ROC Curve | Area Under Curve False Positive Rate vs True Positive Rate Mahesh Huddar