filmov
tv
Writing a quadratic equation from a graph

Показать описание
How To Find The Equation of a Quadratic Function From a Graph
Writing Quadratic Equations from Tables
Writing a Quadratic Function from Points (Example)
Writing a quadratic equation from a graph
Determining the quadratic equation given a vertex and a point
Writing Quadratic Equations from a Graph Tutorial
Ex: Find the Equation of a Quadratic Function from a Graph
Writing Quadratic Equations In Standard Form Given The Solution
Engineering Mathematics: Algebra [Quadratic Equations]
Standard Form to Vertex Form - Quadratic Equations
How To Solve Quadratic Equations Using The Quadratic Formula
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Writing a Quadratic Equation from a Table (Sequence)
Quadratic Equations - Formulas and Notes
Writing Quadratic Equations from Tables Without 0 for X
Write a Quadratic Equation in Standard Form by Completing the Square (3 Examples)
How to write quadratic equation from table
Three Forms of Quadratic Equations
Example 4: Applying the quadratic formula | Quadratic equations | Algebra I | Khan Academy
Writing the equation of a quadratic function given its graph
Writing an equation in vertex form from quadratic form
quadratic equations in every day life!
Write the Quadratic Equation Given Quadratic Formula
Solving Quadratic Equations using Quadratic Formula - Quadratic Equations
Комментарии
 0:09:35
0:09:35
 0:08:45
0:08:45
 0:07:23
0:07:23
 0:04:37
0:04:37
 0:05:28
0:05:28
 0:04:23
0:04:23
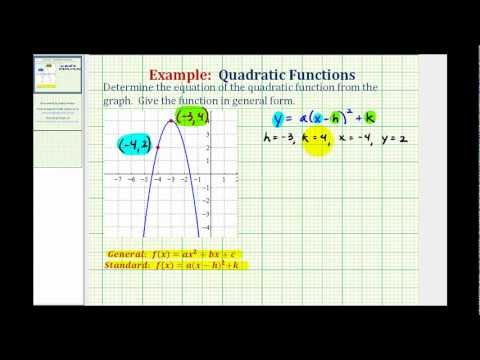 0:04:56
0:04:56
 0:12:50
0:12:50
 0:06:12
0:06:12
 0:02:43
0:02:43
 0:05:56
0:05:56
 0:12:29
0:12:29
 0:11:12
0:11:12
 0:12:01
0:12:01
 0:06:49
0:06:49
 0:05:47
0:05:47
 0:03:13
0:03:13
 0:06:31
0:06:31
 0:05:53
0:05:53
 0:02:29
0:02:29
 0:05:52
0:05:52
 0:05:11
0:05:11
 0:01:49
0:01:49
 0:09:06
0:09:06