filmov
tv
Cannot divide by zero!

Показать описание
We cannot divide by 0, see it by using long division.
Why can't you divide by zero? - TED-Ed
The REAL reason you can't divide by zero
Dividing by zero?
What happens when you divide by zero on a mechanical calculator?
Problems with Zero - Numberphile
Cannot divide by zero!
The real reason why you can’t divide a number by 0!! #math #maths #mathematics #shorts
Why can't you divide by zero?
Lesson 24: Computational Game Theory by Mohammad Hajiaghayi: Shapley Value in Coalition Game Theory
Dividing by Zero in Five Levels -- Elementary to Math Major
CANNOT Divide By 0
why you can't divide a number to zero? #facts #science #technology
Why YOU CANT Divide by ZERO!! #viral #maths
Why can't you divide by 0? Animation vs Math
Why can't we divide a number by ZERO?
Dividing by 0? #programming #computerscience
Actually, you CAN divide by zero.
What Happens if you Divide by Zero on Different Calculators?
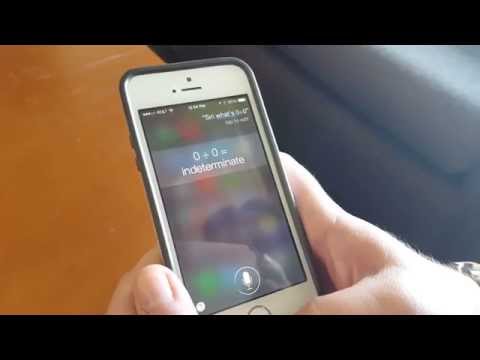
Sassy Siri: 'What's zero divided by zero?'
Why you Cannot Divide by Zero
1 divided by 0 (a 3rd grade teacher & principal both got it wrong), Reddit r/NoStupidQuestions
Why can't you divide by zero?
0 divided by 0
Rule #37: You cannot divide by zero
Комментарии
 0:04:51
0:04:51
 0:01:39
0:01:39
 0:09:09
0:09:09
 0:00:40
0:00:40
 0:13:00
0:13:00
 0:05:44
0:05:44
 0:01:00
0:01:00
 0:02:49
0:02:49
 0:59:12
0:59:12
 0:06:49
0:06:49
 0:00:48
0:00:48
 0:00:50
0:00:50
 0:00:15
0:00:15
 0:00:45
0:00:45
 0:02:58
0:02:58
 0:00:33
0:00:33
 0:03:52
0:03:52
 0:08:20
0:08:20
 0:00:21
0:00:21
 0:05:29
0:05:29
 0:04:52
0:04:52
 0:00:58
0:00:58
 0:00:07
0:00:07
 0:00:07
0:00:07