Proving Trig Identities but they keep getting HARDER | jensenmath.ca

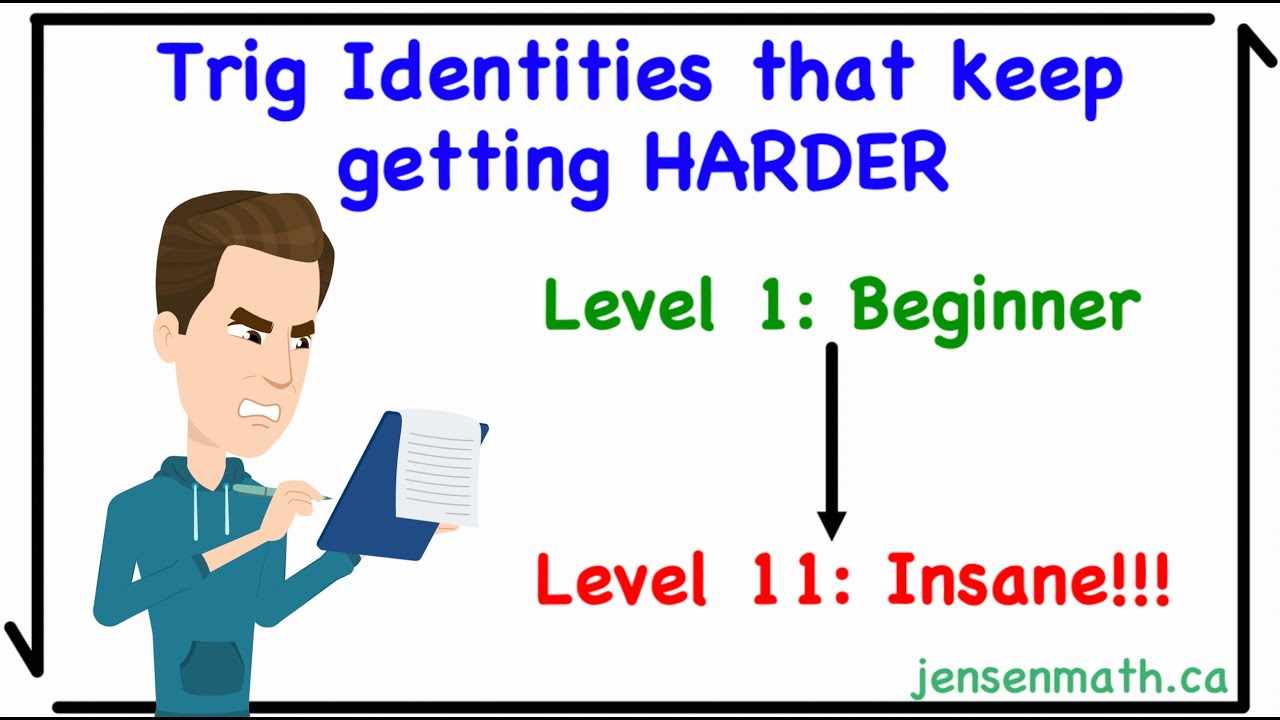
Welcome back to JensenMath! In this video, we're diving deep into the fascinating world of trigonometric identities, but with a twist – they're getting harder and harder as we progress! Whether you're a seasoned math enthusiast or just starting out, this video will put your trigonometry skills to the ultimate test.

Join me as we tackle 11 challenging trig identity proofs, ranging from the relatively straightforward to the mind-bendingly complex. From basic trigonometric relationships to advanced manipulations, we'll explore a wide range of techniques to unravel these identity puzzles.

As always, my goal is to provide clear and concise explanations to help you understand each step of the process. Whether you're following along for the challenge or seeking to deepen your understanding of trigonometry, there's something for everyone in this video.

So grab your pen and paper, sharpen your analytical skills, and let's embark on this trigonometric journey together! Don't forget to pause the video and attempt each proof yourself – how far will you get before needing a hint?

0:00 level 1
0:52 level 2
2:32 level 3
3:39 level 4
4:59 level 5
6:05 level 6
6:54 level 7
8:46 level 8
10:40 level 9
12:53 level 10
14:27 level 11

#Trigonometry #MathProblems #JensenMath

[jaredgage]

I failed high school math used your videos to get my courses and now am headed off to become a electeician much love from waterloo canada

[neVheawastaken]

The last one can be done by
sec⁶x-tan⁶x
sec⁶x-(tan²x)³
sec⁶x-(sec²x-1)³
sec⁶x-(sec⁶x-3sec⁴x+3sec²x-1)
3sec⁴x-3sec²x+1
1+3sec²x(sec²x-1)
1+3sec²xtan²x
which is a more elegant solution

[promessekabongo]

This is very helpful and always fun to study along! Would it be possible to recreate this but in calculus version? Like “calculus problems but they increasingly get more difficult”?

[hjn]

Me watching even tho I couldn’t even do the first one

[gianlucacaforio]

I enjoyed them all! Everyone on first try, the last one on my third. Thank you❤❤

[Kishblockpro]

For the last one I think after the factorisation it’s simpler to add and subtract 1, leave the sec^2xtan^2x term alone and then you can quickly get the rest you need, the reason adding and subtracting one is obvious is because on the right side it means you can make the differing two terms the same with he extra one, this allowed me to solve the problem in my head very quickly without much ugly manipulation

[idonthaveaname]

I recently discovered your channel and it’s been very helpful. Thank you for your work!

[abhiramsridhara]

All done! For the last identity we can use, a³-b³= (a-b)³ + 3ab(a+b).

[IcycleBicycle]

The fact that the second one was with some SEC trigonometric function that I have never ever seen even though I am studying calculus 1 is insane😂😂

[安妮Bei]

Thank you for the video! It was a much needed refresher on trig identities.

[Cool_Name_]

Level 8 can be done easier by using cos^2(x)=1-sin^2(x)
So we get
(1-sin^2x)/sinx(1-sinx) -1
(1-sinx)(1+sinx)/sinx(1-sinx) -1
1+sinx/sinx -1
cscx+1-1
cscx

[呂仲肥]

For level 9, just divide the LS with cosxcosy separately

[coocow]

franchement chanmé le compte ça fait bien bosser le cerveau là merci le boss

[bouazabachir]

Thanks a lot professor I follow you from Algeria. Mes salutations. Bonne continuation professeur

[thomasolson]

The right side of #9, (1+tanx*tany)/(1-tanx*tany) is the tangent addition formula (a+b)/(1-a*b). Where one of them is 45 degrees and the other something else. It seems to come up when I'm playing with complex numbers in trig functions and change of basis. I wasn't aware of the cos(x-y)/cos(x+y) relationship.

[Sgth]

For level 4, I used the LHS. Factored out sin^2(x) and it became sin^2(x) ( sec^2(x) - 1)

sec^2(x) - 1 is an identity, which is equal to tan^2(x).

sin^2(x)tan^2(x)

[MrAlec]

for the last one

LHS = s^6 - t^6 = (1 + t^2)^3 - t^6 = 1 + 3t^2 + 3t^4 = 1 + 3t^2( 1 + t^2) = 1 + 3t^2s^2 = RHS

[quakers]

If you use other trig rules shouldn't they be proved also? There are values of x that clearly breaking the divide by zero rule. Should they be taken into account during the proof or just sta ted at the end of do we just assume they are part of the identity ?

[mathisnotforthefaintofheart]

While cross multiplication is frowned upon in proving identities, the principle of addition in equations can still be used without any loss of validity or rigor. So in example 8, the problem would have been greatly simplified if 1 got added to both sides. Making a common denominator with that minus 1 does not add anything to the proof.

[ingiford]

The first 'identity' is not true. At Pi/2, the LHS is 1, while the right is undefined and is undefined. It is undefined for Pi/2 + n * Pi, where n is an integer; while the LHS is always defined.