filmov
tv
0,999999 ... = 1 ?

Показать описание
Est-ce que 0,999... (avec une infinité de 9) est égal à 1 ?
Cette vidéo apporte une réponse et met en place la notion de développement décimal propre d'un nombre réel.
Niveau première année d'enseignement supérieur scientifique.
Lien vers la vidéo sur la partie entière :
00:00 Introduction
00:38 Développement décimal d'un réel : première approche
01:26 Convergence d'une série du type sum (c_n * 10^(-n), n=1..∞)
04:19 Réponse affirmative à la question : 0,999... = 1 ?
05:08 Développement décimal propre (approche théorique)
09:13 Problème d'unicité, Nombres décimaux
10:29 Conclusion
Cette vidéo apporte une réponse et met en place la notion de développement décimal propre d'un nombre réel.
Niveau première année d'enseignement supérieur scientifique.
Lien vers la vidéo sur la partie entière :
00:00 Introduction
00:38 Développement décimal d'un réel : première approche
01:26 Convergence d'une série du type sum (c_n * 10^(-n), n=1..∞)
04:19 Réponse affirmative à la question : 0,999... = 1 ?
05:08 Développement décimal propre (approche théorique)
09:13 Problème d'unicité, Nombres décimaux
10:29 Conclusion
Does 0.999... = 1?
I'm Settling This Math Debate Forever (.99 repeating = 1)
3 PREUVES QUE 0,9999... = 1 🤯
Every PROOF you've seen that .999... = 1 is WRONG
Among Us in HD (Part 89) SHRINK LOOP #Shorts
0,99999... = 1 ? Três maneiras de mostrar que é verdade!
¿ ES 0´9999 IGUAL A 1? 🤔 #shorts #derivando #matematicas
Почему 0 в степени 0 равно 1?
¿Es 0’9999999… igual a 1?
0,999999... é igual a 1 prova por Soma Infinita! | Dicas A+
0,99999999... = 1 ? (in 60 seconds ?)
0,9999... = 1 !!!
0,999999.... = 1 ?
Grenzwerte Verstehen oder Warum ist 0,99999....=1
0,999999 ... = 1 ?
the Vecna transformation is 🤯 #shorts #strangerthings #netflix
0,99999999.... Sayısı 1'e Eşit Midir ?
La preuve que 0,99... = 1 et ne cherchez pas l'erreur !
Montrer que 0.9999...=1. Montre que 0,999999=1. nombres réels. nombres rationnels 0.3333333= 1/3
D14 Ich kann erklären, dass 0,999999… = 1 ist
Pourquoi 1=0,999999999... ?
TE MOSTRO EM 1 min | 0,999999...=1 - Ep.35
0,9999... = 1? Mais uma aplicação dos limites!
PQ 0,999… = 1 EXPLICADO em 3 níveis diferentes
Комментарии
 0:02:27
0:02:27
 0:04:11
0:04:11
 0:09:35
0:09:35
 0:09:25
0:09:25
 0:00:08
0:00:08
 0:10:13
0:10:13
 0:00:49
0:00:49
 0:06:28
0:06:28
 0:05:14
0:05:14
 0:01:15
0:01:15
 0:03:24
0:03:24
 0:00:55
0:00:55
 0:00:45
0:00:45
 0:17:34
0:17:34
 0:11:08
0:11:08
 0:00:40
0:00:40
 0:05:24
0:05:24
 0:14:05
0:14:05
 0:01:09
0:01:09
 0:01:29
0:01:29
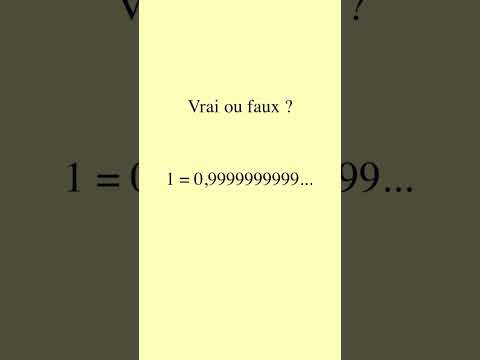 0:01:00
0:01:00
 0:01:00
0:01:00
 0:08:04
0:08:04
 0:06:00
0:06:00