Use calculus, NOT calculators!

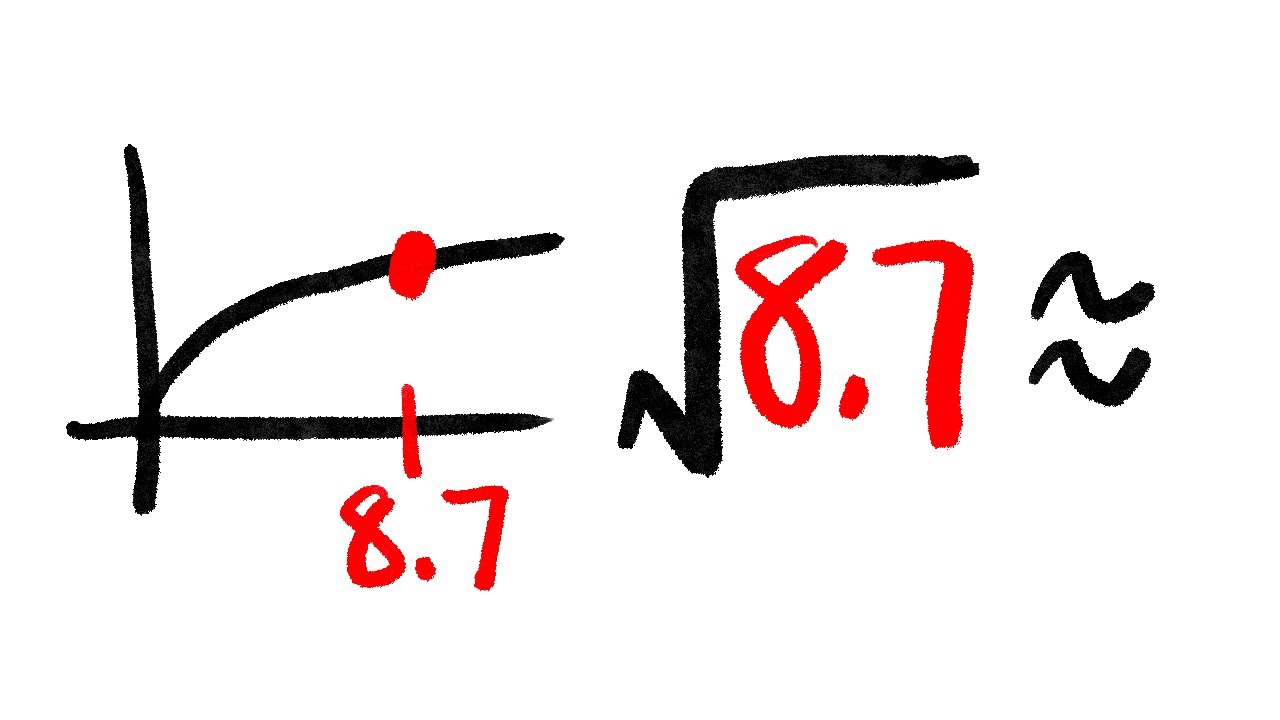
Use calculus, NOT calculators! We will use a tangent line approximation and differentials to approximate sqrt(8.7). This is called local linear approximation, an application of derivatives in Calculus 1.

0:00 use tangent line approximation for sqrt(8.7)
4:49 use differentials to approximate sqrt(8.7)

-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math

[knochentrocken]

Just here to mention that the square root function is a function whose slope gets lower lower and (albeit always bigger than 0), so this means, this method works incredibly well for larger x

[_minhtai_b]

The way he switches his markers is so smooth

[anshumanagrawal]

It's worth mentioning here that the two methods are completely equivalent

[alberteinstein]

This differential method was very interesting to see. I’ve never seen a differential used like this before, thanks for showing this to us!!!

[bollyfan]

I used Algebra, which is much much easier
3^2 = 9 > 8.7
(3 - x)^2 = 8.7
3^2 - 2 * 3 * x + x^2 = 8.7
9 - 6 x + x^2 = 8.7
6 x - x^2 = 9 - 8.7
6 x - x^2 = 0.3
Since x is very small, x^2 <<< 6 x and hence x^2 term can be ignored as an approximation
6 x = 0.3
x = 0.05
so square root of 8.7 = ~(3 - 0.05) = ~2.95

[skylardeslypere]

If you work out the differential method for a general function y=f(x), you eventually get the exact same result, namely that f(x) ≈ f(x*)+f'(x*)(x-x*)

[martinepstein]

How I think about it: The derivative of sqrt(x) is 1/(2sqrt(x)) so the derivative at x = 9 is 1/6. So by definition of the derivative

sqrt(9 + h) = sqrt(9) + h/6 + o(h) ~ 3 + h/6

Now plug in h = -0.3 to get

sqrt(8.7) ~ 3 - 0.3/6 = 2.95

[l.i.a.m.b]

Can we appreciate how smoothly he switches markers?

[seapanda]

Thank you, I'm currently trying to learn calculus by myself and these videos help increase my understanding about the topic

[sabyasachichoudhury]

Wait.
You could improve this method by using it recursively, right?
So, for example, to find the root of 8.7, instead of just using the derivative at 9, you could use the derivative at 9 to find the root of 8.9.
Then using use root 8.9, find root 8.8, and then finally reach 8.7.
That should, in theory, provide a closer approximation.

[stapler]

Differentials are strange objects.
In their original meaning they are infinitesimals, which mathematicians came to frown on. In modern mathematics they mean a lot of different things, including linear approximations. In first-year derivatives they pretend to be a ratio, but with limited algebraic properties. In integral notation they just kind of sit there as a reminder that we're dealing with limits, and otherwise just provide some mental shortcuts for manipulating differential equations.
And then it becomes the Jacobian, and so on...

[Arcticroberto]

I'm gonna put this in excel and iterate it quickly, that way I don't have to use a calculator

[GRBtutorials]

Yet another equivalent method is to use the first order Taylor series at 9:
f(x) ≈ f(a) + f'(a)(x-a)
sqrt(8.7) ≈ sqrt(9) + (8.7-9)/(2*sqrt(9)) = 3 - 0.3/6 = 3 - 0.05 = 2.95

It’s equivalent to the two methods shown in the video, but more direct.

[kradius]

Blew my mind, love to see the many methods out there that are typically overlooked

[JesusMartinez-zuxl]

This is so awesome! Finished Calculus 1 and just love watching calculus videos now😅

[let]

i just learnt this in my calc class last week but you made me understand it way more, tqsm

[gpn]

It's great how you showcased both methods to the one problem in a single video. It would also be good to know whether the two methods are always interchangeable, or whether there are problems where only one of the two methods can be applied. Thanks!

[ygalel]

I really loved this concept.

I actually like to use quadratic approximation for one step closer.

[theblackherald]

Just to add that this is a straightforward extension with limits of the secant line method where m = (3 - 2)/(9 - 4). This method gives you the decent approximation sqrt(8.7) = 2.94

[davegoodo]

Thank you! You have a very refreshing style. Using the differential was very insightful.