No Calculus Needed?! How to Maximize Range Using Simple Geometry.

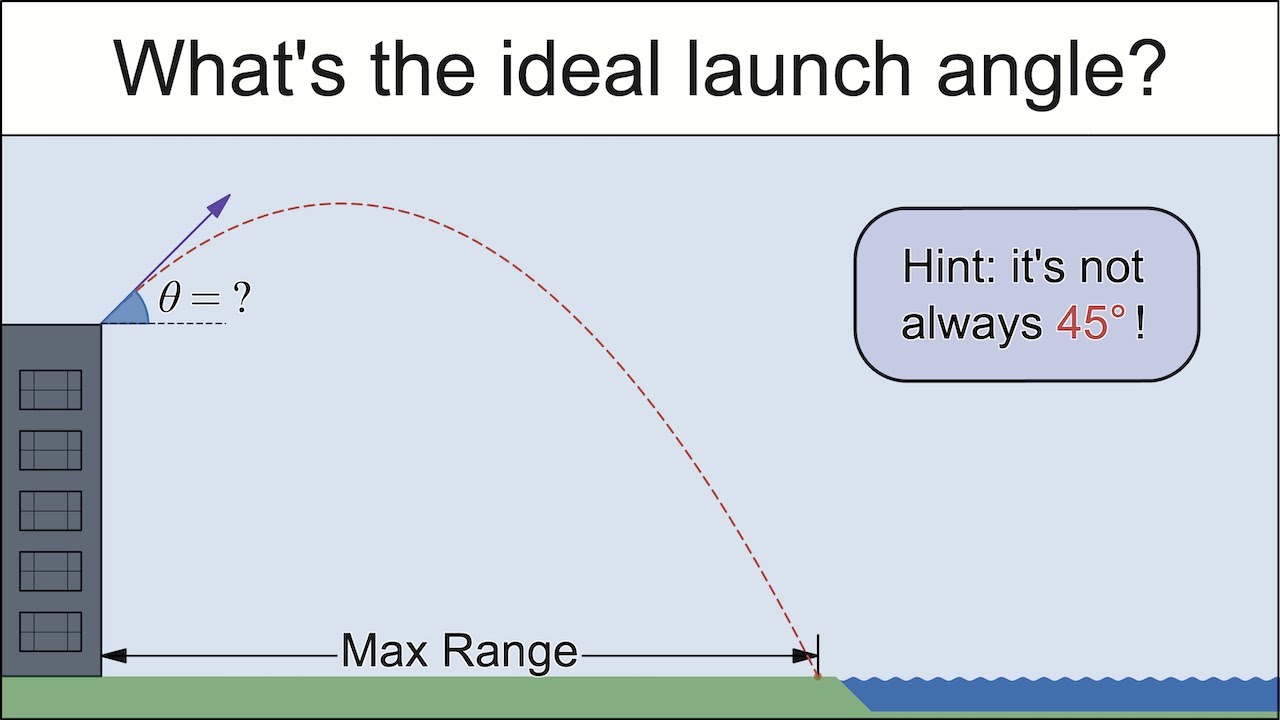
This physics problem, determining the launch angle that gives the maximum range when the starting point is above the level ground, is a personal favorite since it took me a year of cogitating to come up with this solution. No, I never threw anything off a building, but I heard about some rowdies who did, and that is what got me to thinking about this problem.

Of course, ignoring air resistance and other complicating factors means this is just an approximation (and quite possibly a bad one), but accuracy not the point. Such simplifications are useful for teaching the basic concepts of physics and geometry, and for the simple pleasures of exploring the mathematics involved.

BTW, please do not throw things off of buildings! Also, if you throw anything into a body of water, make sure it's natural, not trash.

The method I came up with to solve it involves no calculus or quadratic equations. All you need is elementary physics (conservation of energy, plus basic velocity vector concepts) and some elementary geometry (area of a triangle, simple trig functions). I can't be the only person to come up this solution, but I have have never found anyone who has seen it before. All the websites and videos about this problem use calculus and complicated trig identities. And none of them point out that the denominator in the answer is the final velocity of the projectile. If anyone has heard of this solution, please let me know in a comment.

Update: Commenters have pointed out that this solution is well known by Russian Physics Olympiad competitors.

Corrections:

1:35 “Ray” is the wrong term here. Velocity is represented by a “vector”. A ray doesn’t have a specific length. It extends infinitely in one direction.

[SlimThrull]

"Whatever you can solve with calculus, I can approximate with algebra."

[adityabhandari]

I had asked a question on Physics Stack Exchange, "Why does the optimal angle depend on velocity?" Where someone answered (then suddenly deleted) and told me to check out this video. And this is a video, really nice solution. Thank you!

[tsawy]

I've tried to answer this question at least 4 times in my life, with a focus on the intuitively obvious but interesting fact that the launch angle approaches 0° as the height increases. I think I managed that small problem, but frankly it wasn't very rigourous. This is grand!

[nightsout.]

What I like about the end result is that it still works for the H=0 case (when you're on the ground), and you still get 45 degrees! Great video!

[vishalmishra]

In India, under CBSE board, the Physics NCERT books had (and perhaps still do) what are called star-problems. They are unusually hard problems not meant for everyone but only meant for students who are pretty confident about their physics and math skills (in this context - classical mechanics and differential calculus skills). I ran into this problem for the first time few decades ago and ended up solving it the hard way. Happy to see that there exists a simple and elegant solution for this seemingly easy but actually a pretty hard problem !!

[andrewwilmot]

I remember a certain person posing this exact question 30-some odd years ago in a work office in Bethesda. Nice analysis!

[shiinzshiro]

I love how geometry has a solution to everything.
Triangles, triangles everywhere I look

[MathyJaphy]

One thing missing from the video's narrative is that our little stick figure is throwing as hard as it can. It wouldn't be a very interesting problem if it could "just throw harder", as so many commenters have suggested. :-)

[empty]

this is actually super useful for calculating maximum trajectories when developing a video game, since most video games ignore air resistance for projectiles.

Technically you can just simulate the whole projectiles path, but this is more efficient and would take way less code, awesome!

[NexusEight]

Good stuff MJ. Never thought to have pondered further beyond the "45degrees is the best angle to kick/throw a ball". Luckily I came across this video because not only did you answer a question with great intuition, but you also, and more importantly, thought to have asked a terrific question. Great Job!

[KazeN]

This is really really cool, but a few times you've treated the length of a vector to be the same as the vector itself. That obfuscated the fact that we still don't have an actual formula that can be solved exactly by plugging in the variables at the end here. Would be cool to investigate this a bit more.

[backyard]

What a genius solution! I would've gone brute force calculus and then get stuck trying to solve for the angle

[RannyBergamotte]

My mind is absolutely blown. This is so elegant and wonderful. Keep up the good work!

[idirkhial]

Wow! For a long time I’ve been trying to find an intuitive way to figure out the 45 deg optimal angle without the equations of motion... and now I’ve stumbled upon a general method for all heights! Thanks a lot!

[TheLaxOne]

I’m glad the YouTube algorithm showed me this video, since I’ve been trying to find an elegant way to solve this problem to explain to my sister without needing calculus. Excellent video!

[secretagent]

i must be always standing on the ground as this presentation is way over my head

[WindMills_]

This was really good video. All the points presented are so intuitive that my mind was in awe. Thanks and got subscribed :D.

[holdenmatheson]

This problem can be re-imagined as maximizing the parabola, which happens when the hypotenuse of your triangle passes through the parabola's focal point. This then necessitates that the starting and ending points are 90 degrees offset.

[jamesorendorff]

I just watched three of your videos consecutively, each more unique and nerdy than the last. This is beautiful stuff, thank you for making it!

[glashoppah]

Beautiful. Analytic geometry has solved a lot of things in front of my eyes that looked like they were going to take a lot more work using algebra or calculus.