filmov
tv
Easy Multiplication trick for BIG numbers.

Показать описание
This trick for multiplication is awesome! Multiply numbers near 100 in under 5 seconds. Remember - you don't need a clickbait title to view this - you are far far better than that! Five minutes - you havre another multiplication math trick up your sleeve!
Here is THE mental multiplication lesson playlist - progressing you through your mental multiplication.
Here is THE mental multiplication lesson playlist - progressing you through your mental multiplication.
Easy Multiplication trick for BIG numbers.
How to multiply ANY numbers the fast way - Fast Math Trick
Fast Multiplication Tricks 2 Digit Numbers
Fast Multiplication Trick | Interesting math tricks #maths #shorts
Multiplication Trick for Big Numbers | Faster Mind Calculation Hack
2 Digit Multiplication easily | Brain Games | Brain Development
Japanese Multiplication - Using Lines
Easy Multiplication Hack!
JAPANESE MULTIPLICATION/ How to multiply by JAPANESE method
Multiplication trick #shorts #maths
Trick To Always Remember Your Times Table (6 to 10)
Mental multiplication in 3 seconds
5 Fast Math Tricks for Multiplication - Mental Math
Fast Vedic Mental Math Tricks - Multiplication 01 | Fast Math | Don't Memorise
How to Do Multiplication Without a Calculator : Math Questions & Answers
The Japanese Multiplication Strategy
Multiplication trick-4. How to multiply big numbers
2 digits fast multiplication trick | Easy and fast way to learn | Shortcut trick to multiply
Fast Mental Multiplication Trick - multiply in your head using base 10
Multiplication Tricks! #math #mathematics #mathstricks #maths #mathhacks
Multiplication trick of two digit number | fast trick | Best trick for fast multiplication | #shorts
Long Multiplication Review 📚 #Shorts #math #maths #mathematics #education #learn #learning #review...
Japanese Multiplication | Multiply using lines | Multliplication Trick | Fast math | Zero Math
Multiplication Tricks - Multiply any Two Numbers in 10 seconds | Math Tricks for Fast Calculations
Комментарии
 0:05:33
0:05:33
 0:08:16
0:08:16
 0:00:34
0:00:34
 0:00:28
0:00:28
 0:06:18
0:06:18
 0:05:49
0:05:49
 0:01:30
0:01:30
 0:00:42
0:00:42
 0:00:28
0:00:28
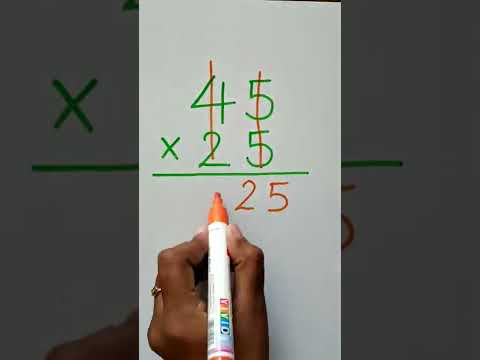 0:00:12
0:00:12
 0:03:25
0:03:25
 0:05:41
0:05:41
 0:07:57
0:07:57
 0:06:11
0:06:11
 0:01:47
0:01:47
 0:07:33
0:07:33
 0:01:38
0:01:38
 0:04:51
0:04:51
 0:10:50
0:10:50
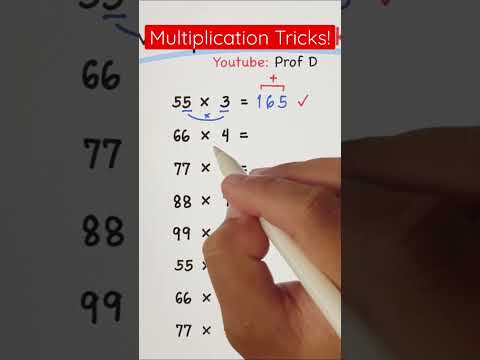 0:01:00
0:01:00
 0:00:58
0:00:58
 0:00:29
0:00:29
 0:07:31
0:07:31
 0:01:00
0:01:00