filmov
tv
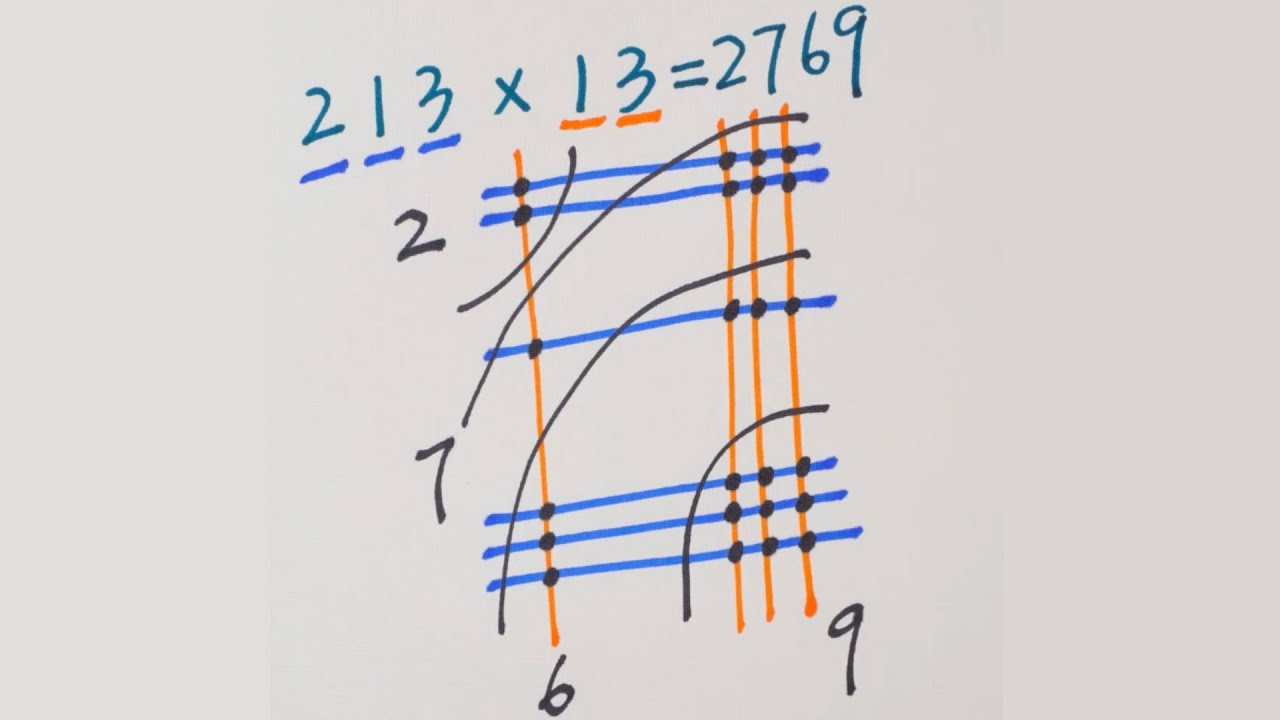
Japanese Multiplication - Using Lines
Показать описание
How Japanese kids learn to multiply in elementary school! 😯
Japanese Multiplication - Using Lines
Japanese Multiplication | Multiply using lines | Multliplication Trick | Fast math | Zero Math
The Japanese Multiplication Strategy
How to multiply using lines | Japanese multiplication | Zero math
Amazing Japanese Multiplication Using Lines! [Math Trick]
Japanese Method in Multiplying Big Numbers Using Lines
How To Do Japanese Multiplication Using Lines-Math Hacks
Line multiplication method | Japanese multiplication | Multiplying numbers with lines
Japanese Multiplication of 4-Digit No.'s Using Lines||#tricks#trick#maths#ytshorts#shorts#vir...
Trikily: Divide two numbers in Japanese technique | Pritam Chakraborty
How to Multiply
Japanese Multiplication - Multiply Using Lines (Math Trick)
JAPANESE MULTIPLICATION/ How to multiply by JAPANESE method
Maths Trick - Multiply Using Lines! | Japanese Technique
Fastest Japanese multiplication method using lines/ Zero number multiplication using Japanese trick
Japanese Multiplication Using Lines
Japanese Multiplication - Methode - Multiply using lines - Utilisation lignes - LvL 1
Math Trick - Multiply Using Lines - Japanese Multiplication
Japanese Multiplication Trick | Multiply using Lines | Short Trick | Faster Calculation
Japanese Multiplication method using lines (Math Tutorial)
How To Multiply Numbers And Algebra Equations By Drawing Lines
Japanese Multiplication | Multiplication trick | How to multiply
Japanese multiplication . Math Trick - Multiply Using Lines! . Math Trick - multiply with lines.
Japanese Multiplication - Using Lines
Комментарии
 0:01:30
0:01:30
 0:07:31
0:07:31
 0:07:33
0:07:33
 0:06:34
0:06:34
 0:07:57
0:07:57
 0:00:45
0:00:45
 0:06:50
0:06:50
 0:04:35
0:04:35
 0:01:00
0:01:00
 0:03:09
0:03:09
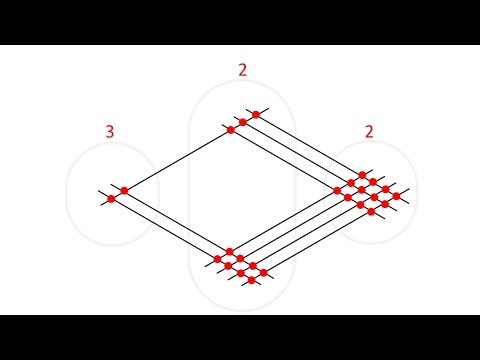 0:04:25
0:04:25
 0:06:27
0:06:27
 0:00:28
0:00:28
 0:05:59
0:05:59
 0:05:38
0:05:38
 0:00:24
0:00:24
 0:01:53
0:01:53
 0:01:56
0:01:56
 0:06:31
0:06:31
 0:08:03
0:08:03
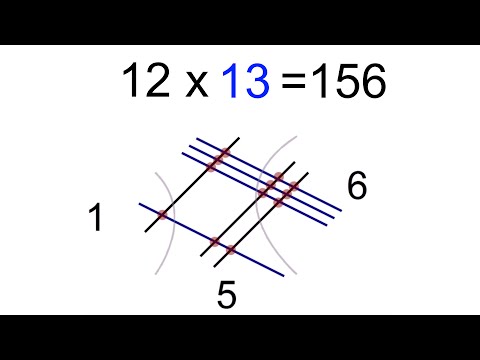 0:04:48
0:04:48
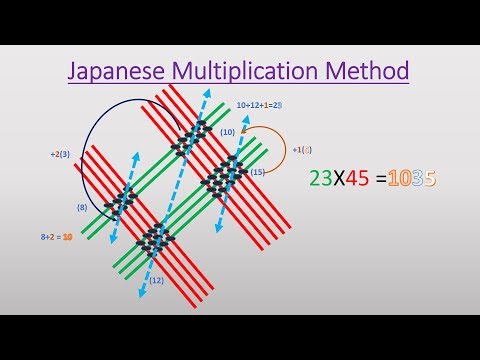 0:02:46
0:02:46
 0:02:46
0:02:46
 0:00:28
0:00:28