filmov
tv
Олимпиадное уравнение по кличке «3 часа». #математика #уравнение #олимпиада #степень #simplemath

Показать описание
Олимпиадное уравнение по кличке «3 часа». #математика #уравнение #олимпиада #степень #simplemath...
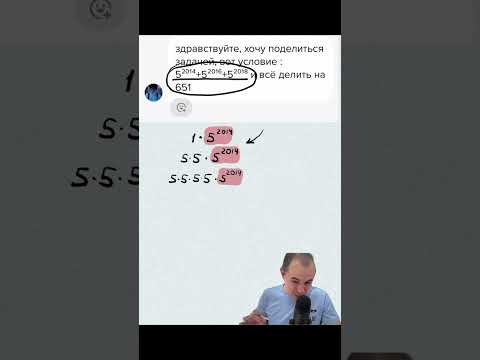
Американская математическая олимпиада. #математика #олимпиада #уравнение #степень #логарифмы...
Уравнение из областной олимпиады #математика #репетитор #репетитор...
Сможешь доказать бесконечность решений? #математика #уравнение #степень #олимпиада #simplemath...
Олимпиадная задача со степенями #математика #арифметика #дробь #степень #олимпиада...
Интересный способ решения. Олимпиадное уравнение
Математика, Олимпиады, 5 класс, Всеросс (ВсОШ), Муниципальный этап, Лен. область 20-21 год, Задача 5...
Итальянская олимпиада за 1 минуту 🍕#математика #егэ2023 #школа #математикапрофиль2023...
МАТЕМАТИКА - олимпиадные задачи! СТЕПЕНИ #shorts
Система по кличке 'Взрыв мозга' (Олимпиадные задачи)...
ПЕРСИДСКАЯ ОЛИМПИАДА 😉 #егэ #математика #профильныйегэ #shorts #огэ...
Математическая матрешка. #математика #счет #корень #умножение #олимпиада #simplemath...
Разбор Интересной Задачи С Неизвестными Степенями | MateMitika...
#RO2023 #RSPC_Daryn #RespublikalyqOlimpiada #JaratylystanuMatematikalyqBağyt Республикалық Олимпиада...
Поняли что за «волшебное слово»? #спорт #история #олимпиада #юмор #биатлон...
Олимпиада для 7 класса
Система уравнений для израильского выпускника
Олимпиадная задача про целые числа
'Зверская' система уравнений с животными
Система уравнений
Занимательная Задача С Перечневой Олимпиады | Разбор Перечня По математике | МатеМитика...
Четная функция
Наибольший корень уравнения. Олимпиада по математике
Олимпиадные школы круглый год. Глеб Дильман - Неравенства 3...
Комментарии
 0:00:46
0:00:46
 0:00:57
0:00:57
 0:00:58
0:00:58
 0:01:01
0:01:01
 0:01:01
0:01:01
 0:01:34
0:01:34
 0:00:47
0:00:47
 0:00:59
0:00:59
 0:00:32
0:00:32
 0:14:40
0:14:40
 0:00:59
0:00:59
 0:00:57
0:00:57
 0:01:29
0:01:29
 0:00:16
0:00:16
 0:00:35
0:00:35
 0:00:58
0:00:58
 0:04:16
0:04:16
 0:01:55
0:01:55
 0:03:22
0:03:22
 0:03:14
0:03:14
 0:03:47
0:03:47
 0:01:36
0:01:36
 0:04:38
0:04:38
 0:04:00
0:04:00