filmov
tv
Exponential derivative

Показать описание
In this video, I define the exponential derivative of a function using power series, and then show something really neat: For “most” functions (those that have a power series expansion), the exponential derivative is just shifting the function by 1!
I also derive the product rule for exponential derivatives, which is much more elegant than the one for derivatives.
Enjoy!
I also derive the product rule for exponential derivatives, which is much more elegant than the one for derivatives.
Enjoy!
Derivatives of Exponential Functions
Exponential derivative visual
Derivatives of Logarithmic and Exponential Functions
Derivative of Exponential Function (e^x) From First Principles
What's so special about Euler's number e? | Chapter 5, Essence of calculus
How to differentiate the exponential function easily
The exponential of the derivative?
Exponential functions differentiation intro | Advanced derivatives | AP Calculus AB | Khan Academy
Solve this exponential equation | #exponents #mathproblem #mathstricks
Exponential derivative
Proof of the Derivative of the Exponential Functions
Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions
Derivatives of Exponential Functions
Exponential Derivative ?!
Differentiating Exponential Functions: e
DERIVATIVE OF EXPONENTIAL FUNCTIONS
Derivative of Exponential Functions | Differentiation of e power x | Calculus #Shorts #YoutubeShorts
Differentiating Exponential Functions (1 of 3: A Visual Argument for the Derivative)
Why is the derivative of e^x equal to e^x?
Differentiation of a^x type exponential functions : ExamSolutions
The Derivative of the Natural Exponential Function
Can we exponentiate d/dx? Vector (fields)? What is exp? | Lie groups, algebras, brackets #4
Derivatives of exponential and chain rule
Differentiating Exponential Functions (1 of 2: Reviewing simple derivatives)
Комментарии
 0:12:03
0:12:03
 0:00:57
0:00:57
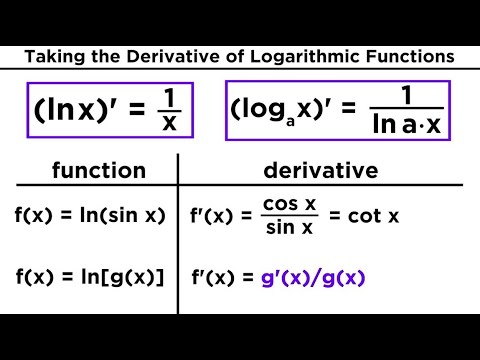 0:08:41
0:08:41
 0:12:33
0:12:33
 0:13:50
0:13:50
 0:03:16
0:03:16
 0:19:08
0:19:08
 0:05:24
0:05:24
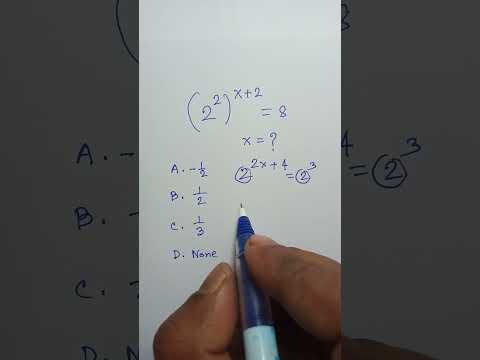 0:00:50
0:00:50
 0:25:53
0:25:53
 0:02:35
0:02:35
 1:30:52
1:30:52
 0:04:36
0:04:36
 0:25:54
0:25:54
 0:05:07
0:05:07
 0:07:39
0:07:39
 0:00:28
0:00:28
 0:10:08
0:10:08
 0:11:59
0:11:59
 0:07:38
0:07:38
 0:09:29
0:09:29
 0:30:09
0:30:09
 0:02:13
0:02:13
 0:11:43
0:11:43