filmov
tv
The exponential of the derivative?

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Derivatives of Exponential Functions
The exponential of the derivative?
Exponential derivative visual
Exponential Derivative ?!
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Exponential functions differentiation intro | Advanced derivatives | AP Calculus AB | Khan Academy
Derivatives of Logarithmic and Exponential Functions
Derivative of Exponential Function (e^x) From First Principles
Exponential Math Problem #math #maths #education #trending #viralvideo #shorts #youtubeshorts
How to differentiate the exponential function easily
Calculus: Find the derivatives! – Exponential functions
Proof of the Derivative of the Exponential Functions
Derivative of exponential function #math
Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions
Derivative Rules for different functions | exponential functions| logarithmic function #mathstricks
Derivative Of Exponential Functions | Differentiation of e power x | Calculas #shorts #youtubeshorts
Exponential derivative
How to Graph Exponential Functions
Derivatives of Exponential Functions
Exponential functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy
DERIVATIVE OF EXPONENTIAL FUNCTIONS
Calculus - Exponential Function Derivative
Derivative of Exponential Functions | Differentiation of e power x | Calculus #Shorts #YoutubeShorts
Derivative - Exponential Function #shorts #maths #differentiation #exponential #derivatives
Комментарии
 0:12:03
0:12:03
 0:19:08
0:19:08
 0:00:57
0:00:57
 0:25:54
0:25:54
 0:13:50
0:13:50
 0:05:24
0:05:24
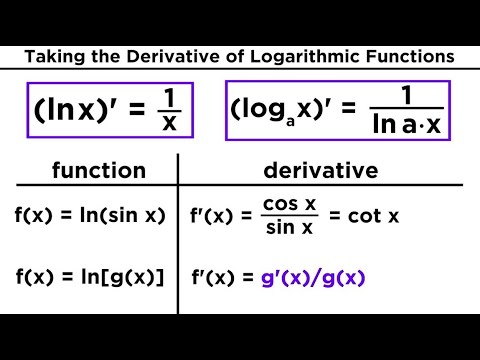 0:08:41
0:08:41
 0:12:33
0:12:33
 0:00:15
0:00:15
 0:03:16
0:03:16
 0:08:45
0:08:45
 0:02:35
0:02:35
 0:00:09
0:00:09
 1:30:52
1:30:52
 0:00:11
0:00:11
 0:00:09
0:00:09
 0:25:53
0:25:53
 0:00:40
0:00:40
 0:04:36
0:04:36
 0:03:39
0:03:39
 0:07:39
0:07:39
 0:03:45
0:03:45
 0:00:28
0:00:28
 0:00:40
0:00:40