filmov
tv
Derivative of Exponential Function (e^x) From First Principles

Показать описание
In this video I showed that d/dx (e^x) = e^x using the definition of the derivative.
Derivative of Exponential Function (e^x) From First Principles
Derivatives of Exponential Functions
Why is the derivative of e^x equal to e^x?
Proof: Derivative of e^x is e^x
How to differentiate the exponential function easily
The derivative of e^x.
Exponential functions differentiation intro | Advanced derivatives | AP Calculus AB | Khan Academy
Ex 1: Derivatives Involving the Exponential Function with Base e
Advancing Calculus Research and Teaching with Wolfram Language
Derivative of Exponential Functions | Differentiation of e power x | Calculus #Shorts #YoutubeShorts
Derivatives of Logarithmic and Exponential Functions
Calculus 1 CH 3 Derivatives (10 of 24) The Exponential Function e^x
Differentiating Exponential Functions: e
Ex 1: Derivatives of Exponential Functions
Derivative of ln(e^-x + x*e^-x)
Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions
Derivative of e^2x (Chain Rule) | Calculus 1 Exercises
Calculus 5.1 Derivatives of Exponential Functions y = e^x
Differentiation - e and ln
Proofs of derivatives of ln(x) and e^x | Taking derivatives | Differential Calculus | Khan Academy
Derivatives of exponential and chain rule
The Derivative of e^x is e^x Proof and Introduction to this Amazing Function
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Ex: Application of the Derivative of an Exponential Function (Rate of Depreciation)
Комментарии
 0:12:33
0:12:33
 0:12:03
0:12:03
 0:11:59
0:11:59
 0:10:24
0:10:24
 0:03:16
0:03:16
 0:02:10
0:02:10
 0:05:24
0:05:24
 0:03:49
0:03:49
 1:24:32
1:24:32
 0:00:28
0:00:28
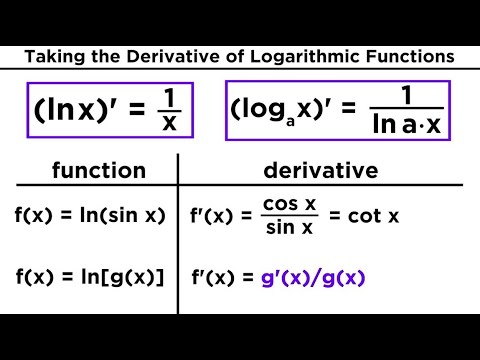 0:08:41
0:08:41
 0:02:48
0:02:48
 0:05:07
0:05:07
 0:02:38
0:02:38
 0:03:29
0:03:29
 1:30:52
1:30:52
 0:00:50
0:00:50
 0:25:59
0:25:59
 0:13:00
0:13:00
 0:12:27
0:12:27
 0:02:13
0:02:13
 0:06:15
0:06:15
 0:13:50
0:13:50
 0:03:43
0:03:43