filmov
tv
Find the sum of coefficients
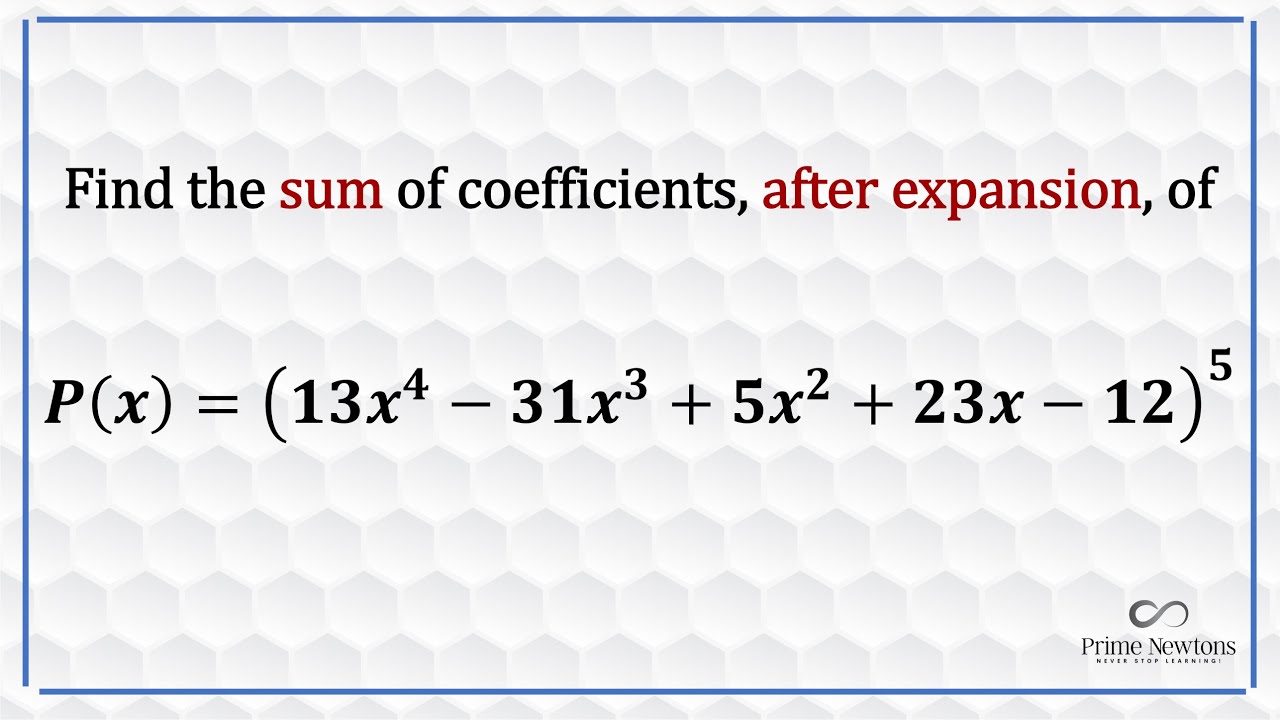
Показать описание
The sum of the coefficients of a polynomial, p(x) = p(1). You may think of it as the remainder when the polynomial is divided by x-1. I did not provide a proof in this video since the purpose is to make the principle known.
Find the sum of the coefficients !
Find the sum of coefficients
ENGINEERING MATHEMATICS: SUM OF COEFFICIENTS OF A POLYNOMIAL EXPANSION
Find the Sum of The Coefficients of (5x^2 - 3y)^2022 | Olympiad Math
How to find sum of coefficients | shortcut method|| IOE entrance question||
What is the sum of all coefficients of this 100th-degree polynomial?
Sum of coefficients of multinomial and binomial expansion | Binomial shortcut
Summing Coefficients of a Binomial Expansion
Sum of Polynomial Coefficients Challenge
Find the sum of coefficients of odd power of x
ACT/SAT Math: Find the Sum of Coefficients of a Quadratic Function Given f(0) and f(1)
How to find the sum of all coefficients in the any expansion .
Sum of binomial coefficients
Finding the Sum of the Coefficients of a Binomial Expansion
Sum of coefficients of binomial expansion|| sum of all coefficients in binomial expansion
What is the sum of the coefficients when the following equation is balanced using the smallest whole
Finding the Sum of the Coefficients of a Binomial Expansion
Find the sum of the coefficients of two middle terms in the|Binomial Theorem|RD Sharma|11|CET|NCERT|
Summing Binomial Coefficients (Exam Question)
JEE Delight: Find the sum of coefficients of integral powers of x in (1-2x^1/2)^50
#62 SUM OF COEFFICIENT OF BINOMIAL EXPANSION FORMULA
Find the sum of the coefficients in the expansion of `(7+4x)^49`
Sum of Coefficients of Polynomial
Find the sum of coefficients in (1+x-3x²)⁴¹⁶³
Комментарии
 0:02:52
0:02:52
 0:05:07
0:05:07
 0:09:28
0:09:28
 0:04:13
0:04:13
 0:04:04
0:04:04
 0:00:46
0:00:46
 0:07:24
0:07:24
 0:02:17
0:02:17
 0:00:37
0:00:37
 0:03:28
0:03:28
 0:00:44
0:00:44
 0:03:26
0:03:26
 0:02:47
0:02:47
 0:03:03
0:03:03
 0:02:49
0:02:49
 0:04:27
0:04:27
 0:07:23
0:07:23
 0:04:32
0:04:32
 0:08:27
0:08:27
 0:02:38
0:02:38
 0:01:50
0:01:50
 0:02:58
0:02:58
 0:03:32
0:03:32
 0:01:00
0:01:00