Propositional Logic and the Algebra of Boole | MathFoundations273 | N J Wildberger

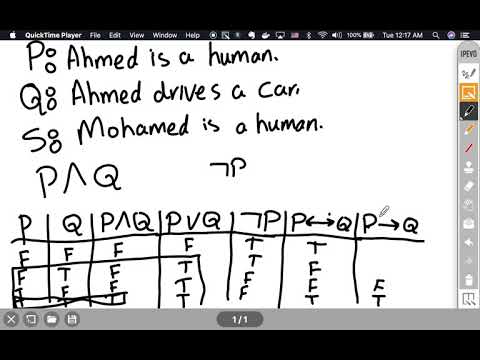
We give an overview of classical Propositional Logic, which is a branch of philosophy concerned with systematizing reason. This framework uses "atomic statements" called "propositions", and "relations", or "connectives", between them, prominently AND, OR, NOT, IMPLIES and EQUIVALENT, and the assumption that these various statements have well-defined truth values, namely "true (T)" or "false (F)". A fun example is a classical puzzle of Lewis Carroll involving your poetry. A statement can be a tautology, contradiction, satisfiable, or debatable (!) depending on what kind of truth values it takes on.

Two main techniques for analysing classical Propositional Logic statements are truth tables and equivalences. We discuss both of these.

However --with the mathematical orientation, initiated by George Boole, we replace "true" and "false" with 1 and 0 respectively, and this then leads to the Algebra of Boole subsuming most of the discussion.

Video Content:
00:00 Introduction
3:28 Lewis Carroll Logic puzzle
6:00 Atomic ingredients
09:05 Truth values: either true (T) or false(F)
13:15 Composite propositions
18:23 Propositional formulas
21:19 Equivalent formulas
25:11 Equivalences are useful
28:01 Three main techniques for simplifying formulas in PL

Here are the Insights into Mathematics Playlists:

Here are the Wild Egg Maths Playlists (some available only to Members!)

************************

[roys]

Another large reason for the rise of Propositional Logic is its role in programming language logics, and software logics more generally. Here it may just be the basics of a larger class of computer logics. Also the formalisation of mathematical axioms in First Order Logic places PL into the introductory category.

[BartWestra]

On sheet 8 starting at 25:12, the two De Morgan rules are written a bit complicated with double negation, like:
r ^ s <-> not ( (not r) V (not s) )
Easier to use for reduction, and more like the distributive laws for ^ and V above would be:
not (r ^ s) <-> (not r) V (not s)
And likewise not (r V s) <-> (not r) ^ (not s)