filmov
tv
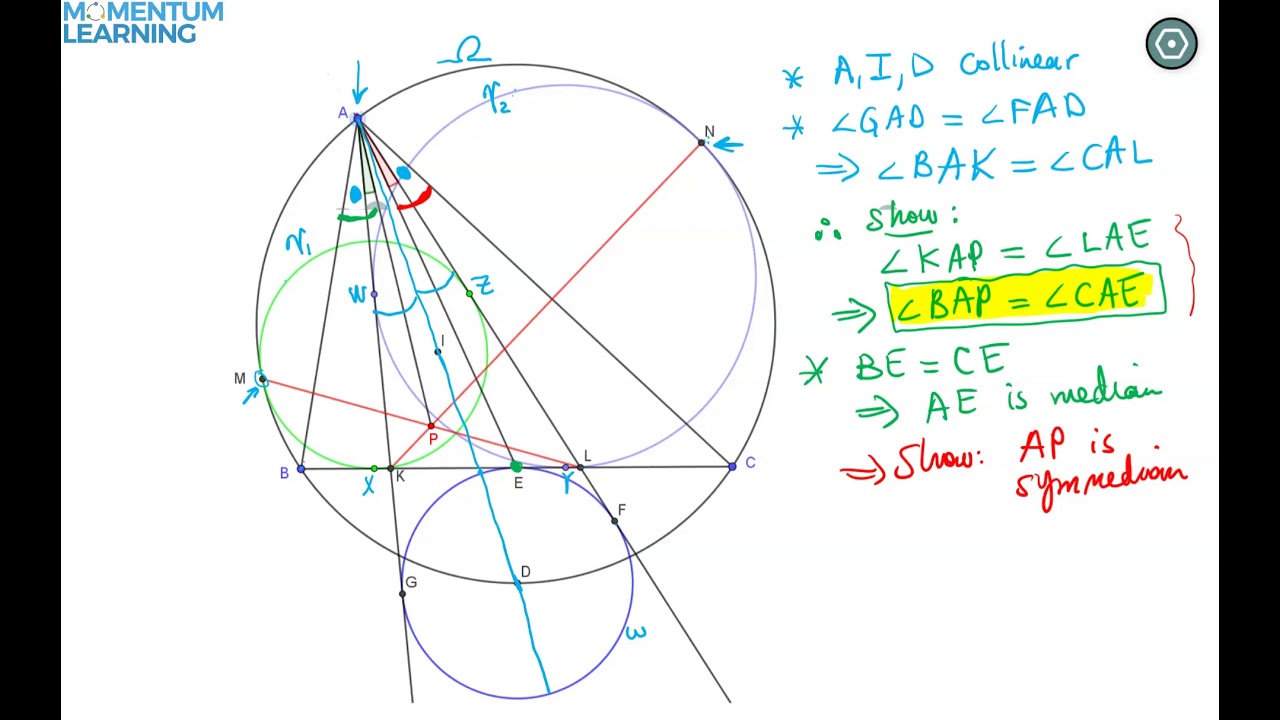
2019 Poland Math Olympiad Geometry problem (Symmedian line, Incenter Excenter Lemma, Monge Theorem)
Показать описание
2019 Polish Math Olympiad
2019 Poland Math Olympiad Geometry problem (Symmedian line, Incenter Excenter Lemma, Monge Theorem)
Poland Math Olympiad Problem | Geometry | 2 Different Methods to Solve
Maths Olympiad Questions - 2019 INMO Q1
Olympiad Geometry Problem #108: Christmas Special - But a Month and a Half Later!
Olympiad Geometry Problem #81: Altitude, Two Circles, Concurrence
A Very Nice Geometry Challenge | Poland Math Olympiad Problem | Find the radius of the circle
Olympiad Geometry Problem #101: Orthocenter Lies on Incircle
Olympiad Geometry Problem #90: Incircle, Midpoint, Equal Angles
2019 USAMO Problem #2 (USAJMO Problem #3)
Olympiad Geometry Problem #98: Circumcenter, Midpoints, Equal Angle
Chinese IMO team
hard geometry problem of polish Mathematical Olympiad
Olympiad Geometry Problem #99: Cyclic Quad, Equal Segment, Parallel
Math Olympiad - Geometry
2018 Poland Math Olympiad Geometry Problem 5 (Two Solutions)
Poland Math Olympiad Problem | A Nice Challenge of Number Theory
Olympiad Geometry Problem #29: Incenter, Perpendicular, Equal Angles
Q24 of SMO 2019 Junior (Geometry: Isosceles triangles)
Olympiad Geometry Problem #88: IMO Shortlist 2019 G6
Math Olympiad: A problem a day... (February 22th, 2019)
Olympiad Geometry Problem #37: IMO 2018 #1
2019 European Girls MO (EGMO) Problem #3
Angle Bisectors and a Math Olympiad Geometry Problem [Geometry]
Olympiad Geometry Problem #8: Perpendiculars, Midpoints, Equal Angles
Комментарии
 0:31:06
0:31:06
 0:11:15
0:11:15
 0:20:49
0:20:49
 0:09:18
0:09:18
 0:15:23
0:15:23
 0:11:40
0:11:40
 0:11:39
0:11:39
 0:08:40
0:08:40
 0:22:59
0:22:59
 0:09:30
0:09:30
 0:00:34
0:00:34
 0:12:07
0:12:07
 0:12:48
0:12:48
 0:04:46
0:04:46
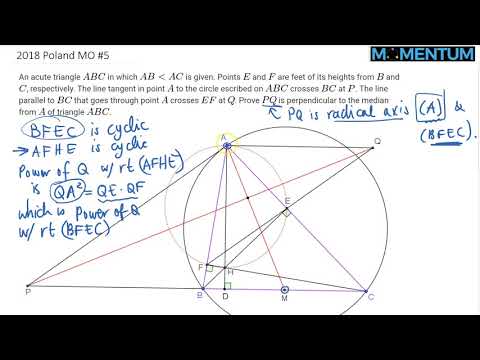 0:34:36
0:34:36
 0:08:24
0:08:24
 0:10:30
0:10:30
 0:03:10
0:03:10
 0:14:51
0:14:51
 0:08:15
0:08:15
 0:10:58
0:10:58
 0:17:53
0:17:53
 0:16:30
0:16:30
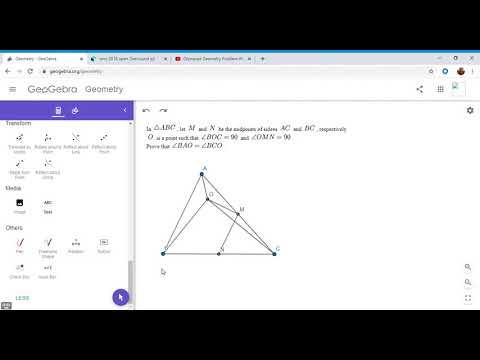 0:08:03
0:08:03