filmov
tv
Olympiad Geometry Problem #8: Perpendiculars, Midpoints, Equal Angles
Показать описание
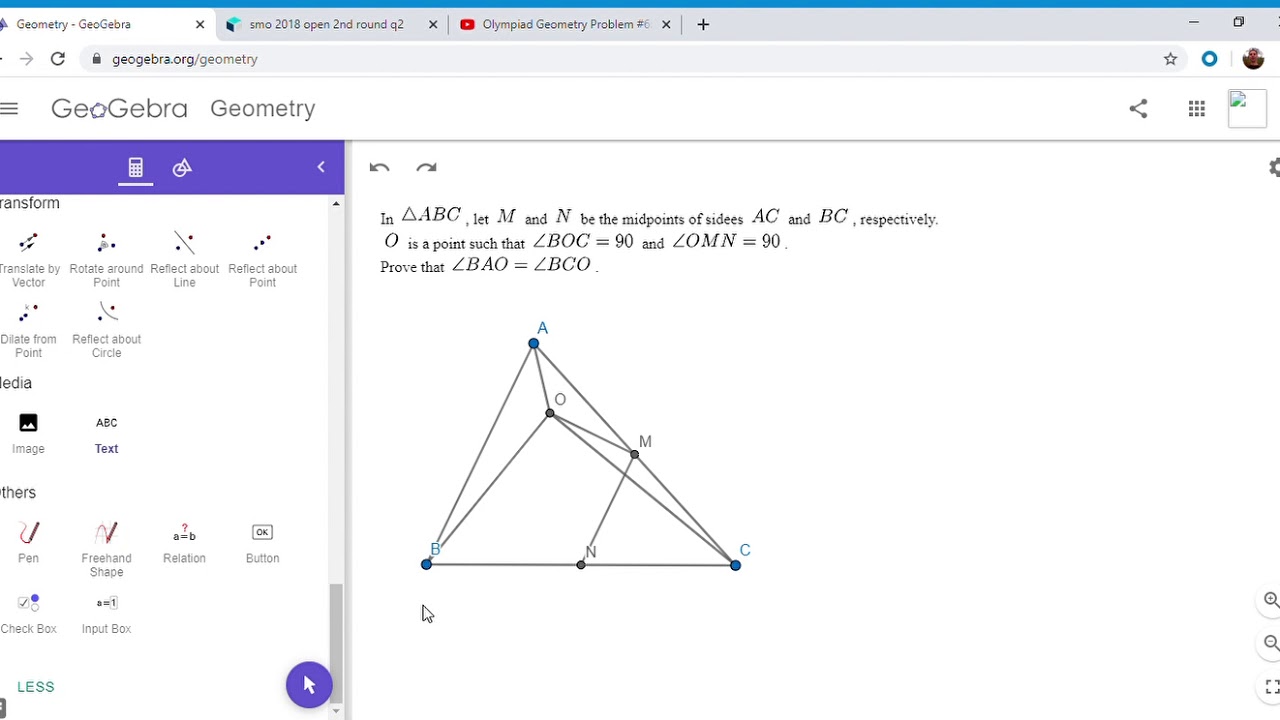
This is a simple but fun problem from SMO 2018. A couple of right angles are given, and you want to use that to show two angles are equal. Enjoy!
Olympiad Geometry Problem #8: Perpendiculars, Midpoints, Equal Angles
Olympiad Geometry Problem #6: Isosceles Triangle, Parallels, Perpendicular
Olympiad Geometry Problem #100: Circumcenter Perpendiculars Cyclic Quad
Olympiad Geometry Problem #30: Incenter, Equal Segments, Perpendicular
Olympiad Geometry Problem #10: Isosceles Triangle, Midpoints, Perpendiculars
Olympiad Geometry Problem #80: Incircle, Reflections, Perpendicular
What is the value x? | Perpendicular Angle Bisectors | 8th Grade Math Olympiad
Olympiad Geometry Problem #89: Reflections, Tangents, Perpendicular
Q481 | Math Olympiad | Geometry | Isosceles Right Triangle | Angle Bisector Theorem
Olympiad Geometry Problem #35: Angle Bisector, Perpendiculars, Tangency
What’s the area?
Olympiad Geometry Problem #99: Cyclic Quad, Equal Segment, Parallel
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Olympiad Geometry Problem #3: Right Triangle, Perpendiculars, Equal Angles
Geometry everyone should learn
Olympiad Geometry Problem #91: Two Perpendiculars, Midpoint, Equal Segments
Lines and Angles Trick | Class 9 Maths Lines and Angles #fun #shorts #mathsiseasy #youtubeshorts
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
Q474 | Math Olympiad | Geometry | 2024 AMC 10B Problem 11 | Triple Perpendicular Similarity Model
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
HOW TO FIND PERIMETER #perimeter #formulae #rectangle #circle #triangle #maths #shorts #ytshorts #yt
Olympiad Geometry Problem #18: Altitudes, Circumcircle, Equal Segments
FULL FORM OF MATHS😍#maths #MATHSFUN#shorts #viral
Last Words of Albert Einstein #shorts
Комментарии
 0:08:03
0:08:03
 0:10:55
0:10:55
 0:07:54
0:07:54
 0:12:29
0:12:29
 0:11:05
0:11:05
 0:13:05
0:13:05
 0:03:09
0:03:09
 0:22:52
0:22:52
 0:03:02
0:03:02
 0:10:33
0:10:33
 0:00:42
0:00:42
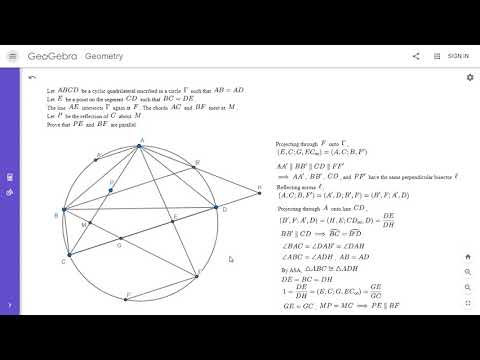 0:12:48
0:12:48
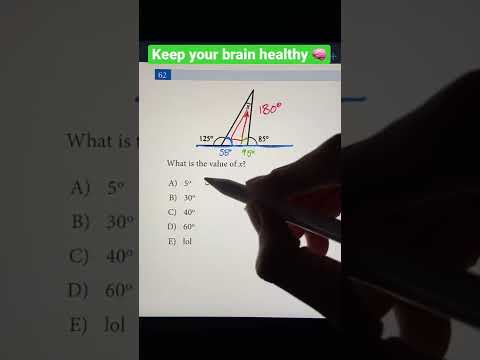 0:00:44
0:00:44
 0:11:20
0:11:20
 0:00:15
0:00:15
 0:13:48
0:13:48
 0:00:34
0:00:34
 0:00:13
0:00:13
 0:03:10
0:03:10
 0:00:37
0:00:37
 0:00:14
0:00:14
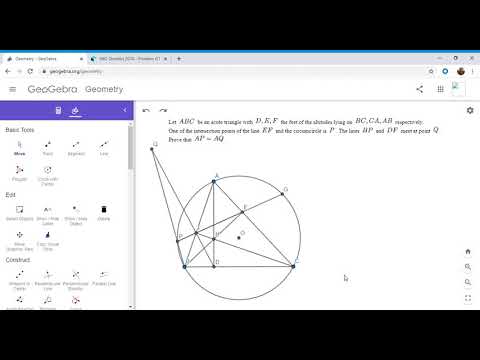 0:12:18
0:12:18
 0:00:41
0:00:41
 0:00:37
0:00:37