filmov
tv
Surface area of a sphere
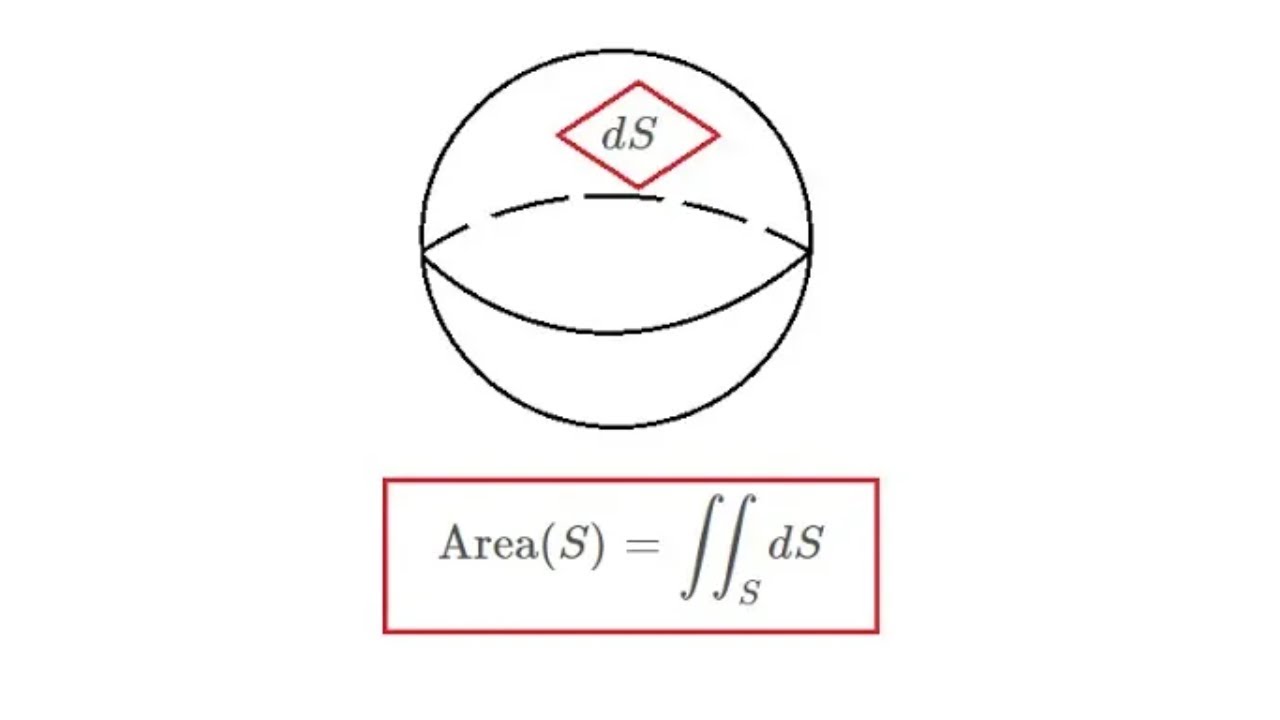
Показать описание
In this video, I show how to find the area of any surface (yes, any surface) by calculating the surface area of a sphere in 3 dimensions. The calculation is absolutely beautiful, because there are 3 amazing simplifications that will happen. Enjoy!
But why is a sphere's surface area four times its shadow?
Surface Area of a Sphere
Volume and Surface Area of a Sphere Formula, Examples, Word Problems, Geometry
Surface Area of a Sphere (equation derived with calculus)
Surface Area of a Sphere explained in easy way | no need to memorise
The surface area of a sphere
How do you find the surface area of a sphere
Surface Area of Spheres (1 of 2: Finding the Surface area of spheres and hemispheres)
the surface area of a solid sphere is 1256 cm square. It is cut into two hemispheres.#a2zmathematics
Surface Area of a Sphere - Nerdstudy
Surface Area Of A Sphere | Geometry | Math | Letstute
Finding the Surface Area of a Sphere
How to Use Surface Area Sphere Formula
Surface Area of Sphere Orange
Why is the surface area of a Sphere 4pi times radius squared???
How To Find The Surface Area Of A Sphere
The Volume of a Sphere - Numberphile
Proving the volume and the surface area of a sphere by using integrals
Deriving Surface Area of a Sphere Using Integration
Sphere Surface Area and Volume
SURFACE AREA of a SPHERE SECTION
Volume and Surface Area of a Sphere | Grade 5 Crossover Playlist | GCSE Maths Tutor
How to Find the Surface Area of a Sphere
Volume and Surface Area of Spheres (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise
Комментарии
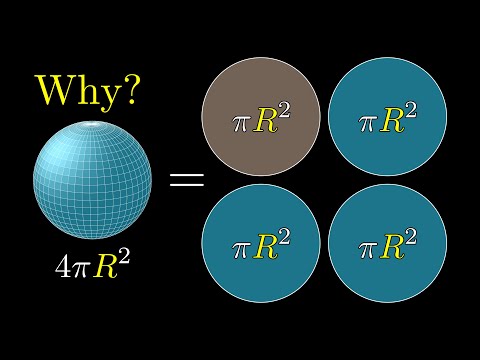 0:15:51
0:15:51
 0:01:20
0:01:20
 0:11:09
0:11:09
 0:05:14
0:05:14
 0:03:45
0:03:45
 0:01:00
0:01:00
 0:01:47
0:01:47
 0:07:23
0:07:23
 0:01:00
0:01:00
 0:02:39
0:02:39
 0:07:40
0:07:40
 0:07:50
0:07:50
 0:03:53
0:03:53
 0:02:58
0:02:58
 0:06:28
0:06:28
 0:07:42
0:07:42
 0:04:14
0:04:14
 0:13:41
0:13:41
 0:07:58
0:07:58
 0:01:55
0:01:55
 0:12:27
0:12:27
 0:13:38
0:13:38
 0:02:35
0:02:35
 0:03:20
0:03:20