filmov
tv
Solving an Interesting Exponential Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentialequations #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentialequations #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving an Interesting Exponential Equation
Solving Exponential Equations
An Interesting Exponential Equation | Math Olympiad
Solving an Interesting Exponential Equation
Solving an exponential equation
Exponential Equations - Algebra and Precalculus
A Very Interesting Exponential Equation | 1ˣ = -1
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving an Exponential Equation | Quick Math Challenge!
I Solved An Interesting Exponential Equation
Can you solve this tricky exponential equation?
An Interesting Exponential Equation
Solving Exponential Equation
A Cool Exponential Equation | Math Olympiads
An Interesting Exponential Equation
5 simple unsolvable equations
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
An Interesting Exponential Equation
How to Graph Exponential Functions
08 - Solving Exponential Equations - Part 1 - Solve for the Exponent
An Interesting Exponential Equation
Solving an exponential equation with different bases
Solving an Interesting Exponential Equation | 9^x+15^x=25^x
Solving exponential equations using exponent properties | High School Math | Khan Academy
Комментарии
 0:08:28
0:08:28
 0:16:36
0:16:36
 0:11:12
0:11:12
 0:08:45
0:08:45
 0:03:14
0:03:14
 0:05:58
0:05:58
 0:01:00
0:01:00
 0:05:12
0:05:12
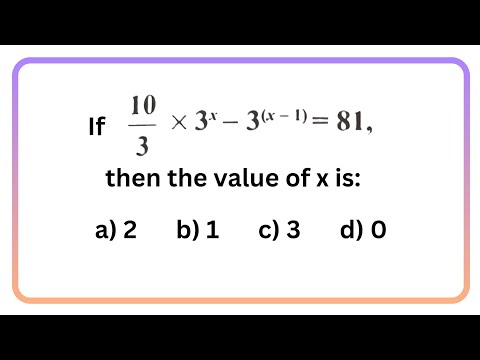 0:04:50
0:04:50
 0:08:10
0:08:10
 0:11:12
0:11:12
 0:04:46
0:04:46
 0:00:56
0:00:56
 0:08:18
0:08:18
 0:08:44
0:08:44
 0:00:50
0:00:50
 0:00:52
0:00:52
 0:13:20
0:13:20
 0:00:40
0:00:40
 0:18:28
0:18:28
 0:08:17
0:08:17
 0:03:01
0:03:01
 0:07:15
0:07:15
 0:04:56
0:04:56