filmov
tv
I Solved An Interesting Exponential Equation
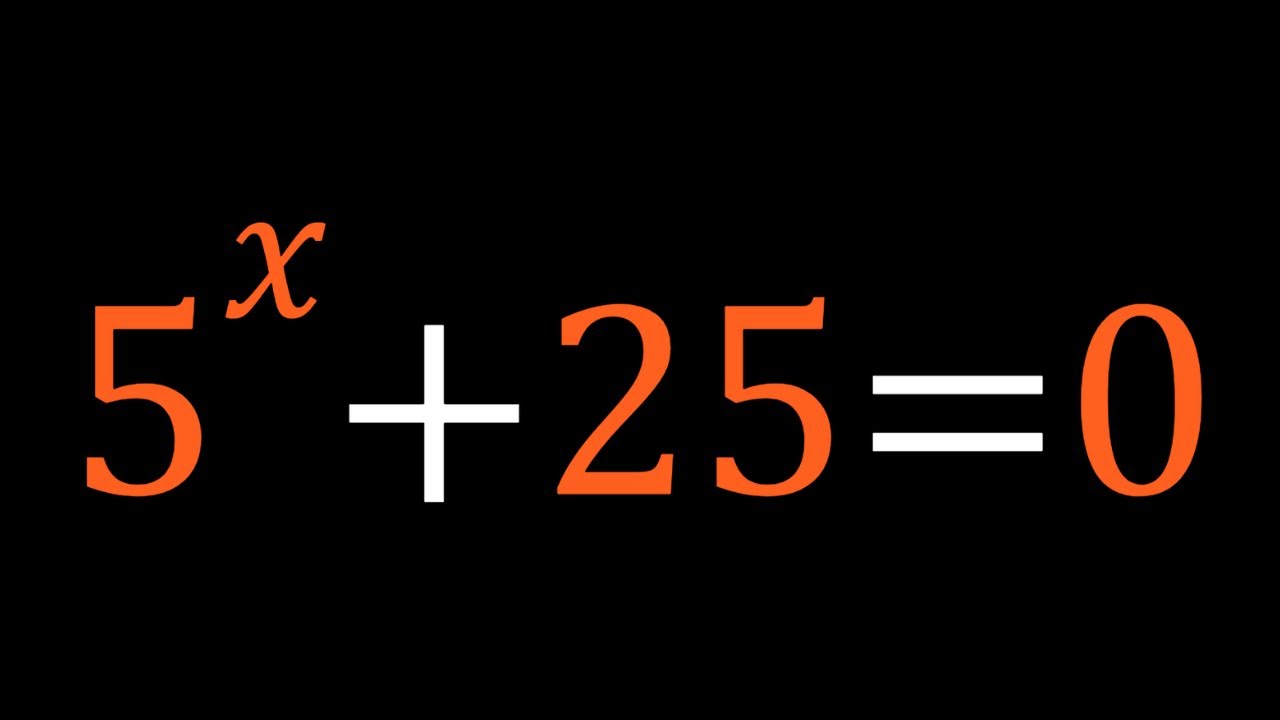
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentials #exponentialequations #algebra #complexnumbers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentials #exponentialequations #algebra #complexnumbers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
I Solved An Interesting Exponential Equation
An Interesting Exponential Equation
Solving an Interesting Exponential Equation
An Interesting Exponential Equation
Solving an Interesting Exponential Equation
Solving An Interesting Exponential Equation
Math Olympiad l A Wonderful Exponential Equation l VIJAY Maths
Solving Exponential Equation
Solving Exponential equations, solve for x
I Solved A Cool Exponential Equation
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A Nice Math Olympiad Exponential Equation 3^x = X^9
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
A Cool Exponential Equation | Algebra
Solving A Quick and Easy Exponential Equation
A Nice Olympaids Exponential Trick | Tricky Math Problem
An Interesting Exponential Equation
Solving Exponential Equations
Very Interesting Exponential Question | Maths Olympiad
An Interesting Exponential Equation
Nice Exponential Math Problem #shorts #maths
An Amazing Exponential Equation | Give It A Try!
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
99% Of People Cant Solve This Simple Problem | A Nice Exponential Problem
Комментарии
 0:08:10
0:08:10
 0:12:11
0:12:11
 0:08:28
0:08:28
 0:08:17
0:08:17
 0:08:45
0:08:45
 0:10:17
0:10:17
 0:07:13
0:07:13
 0:00:56
0:00:56
 0:02:54
0:02:54
 0:09:06
0:09:06
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:00:22
0:00:22
 0:00:25
0:00:25
 0:00:28
0:00:28
 0:08:16
0:08:16
 0:09:45
0:09:45
 0:16:36
0:16:36
 0:05:19
0:05:19
 0:13:20
0:13:20
 0:00:35
0:00:35
 0:11:15
0:11:15
 0:00:28
0:00:28
 0:09:01
0:09:01