filmov
tv
[Calculus | глава 3] Формулы производных через геометрию

Показать описание
[Calculus | глава 3] Формулы производных через геометрию
Формулы производных через геометрию | Суть матанализа, глава 3...
[Calculus | глава 11] Ряд Тейлора
😳 CLEAN BASIC MATHEMATICS 25% of 250=? #Shorts
[Calculus | глава 8] Интегрирование и основная теорема матанализа...
[Calculus | глава 4] Визуализация правила произведения и сложной функции...
[Calculus | глава 12] Другой способ визуализации производных
[Calculus | глава 7] Пределы, правило Лопиталя и эпсилон-дельта определение...
[Calculus | глава 2] Парадокс производной
[Calculus | глава 5] Что особенного в числе Эйлера?
КАК УМНОЖАТЬ ДЕСЯТИЧНЫЕ ДРОБИ? #егэ #огэ #профильныйегэ
[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?...
[Calculus | глава 10] Производные высших порядков
[Calculus | глава 1] Суть матанализа
Высшая математика. Бесконечно малые. В большом количестве #shorts...
Геометрический трезубец
Производная наглядно!#shorts #математика
Визуализация правила произведения и сложной функции | Суть матанализа, глава 4...
Задача 3.195 Сборник задач под редакцией М.Сканави
[Calculus | глава 9] Какое отношение площадь имеет к наклону?
Задача 3.188 Сборник задач под редакцией М.Сканави
Задача 3.198 Сборник задач под редакцией М.Сканави
Помнишь свойства неравенств? #математикапрофиль2024 #егэ2024 #математика #школа #fyp...
Задача 3.194 Сборник задач под редакцией М.Сканави
Комментарии
 0:17:12
0:17:12
 0:17:01
0:17:01
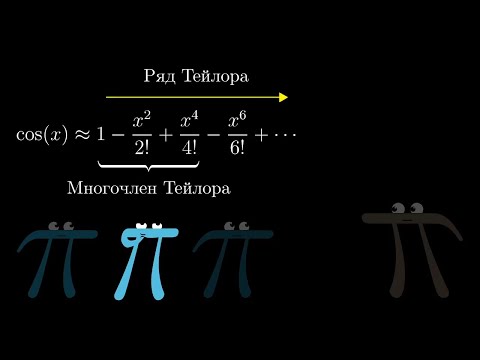 0:21:55
0:21:55
 0:00:24
0:00:24
 0:19:20
0:19:20
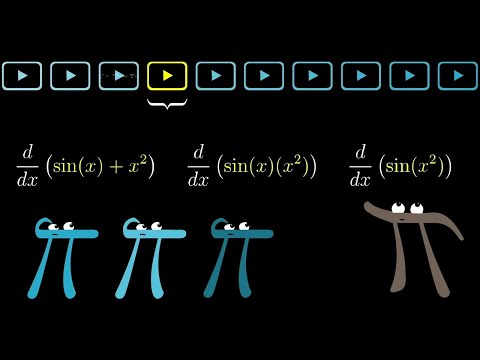 0:15:45
0:15:45
 0:15:41
0:15:41
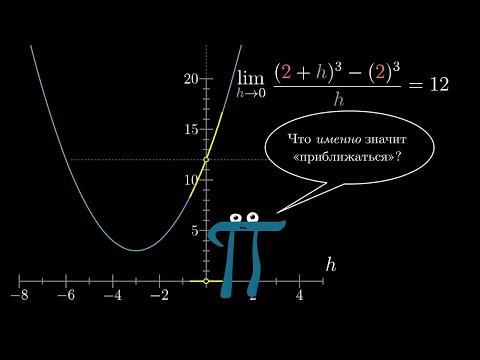 0:17:45
0:17:45
 0:16:41
0:16:41
 0:13:26
0:13:26
 0:00:44
0:00:44
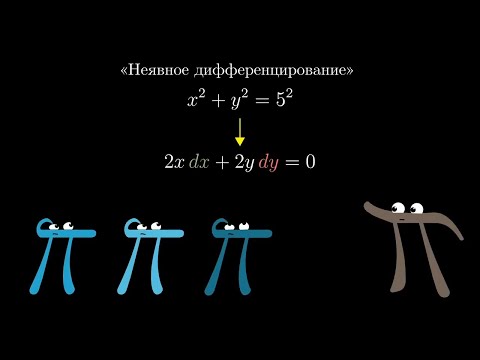 0:15:12
0:15:12
 0:05:29
0:05:29
 0:16:05
0:16:05
 0:00:49
0:00:49
 0:00:36
0:00:36
 0:00:28
0:00:28
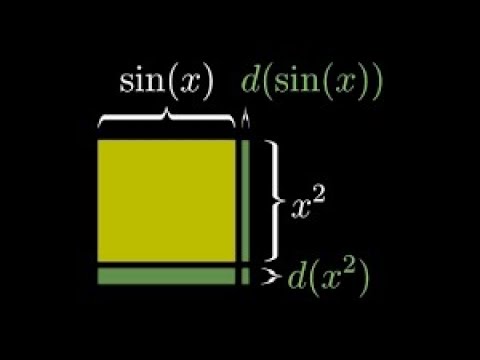 0:15:36
0:15:36
 0:00:21
0:00:21
 0:12:19
0:12:19
 0:00:21
0:00:21
 0:00:31
0:00:31
 0:01:00
0:01:00
 0:00:21
0:00:21