filmov
tv
Two Particle 2D Example, Energy Approach | Intro to Rigid Body of Particles & Kinematics | Lecture 8

Показать описание
Dr. Shane Ross, Virginia Tech. Lecture 8 of a course on analytical dynamics (Newton-Euler, Lagrangian dynamics, and 3D rigid body dynamics). We consider a 2D example of a 2-particle system, in the center-of-mass-centered frame. We use the conservation of total energy and total angular momentum to semi-analytically solve for the relative motion (that is, the motion of the particles relative to the center of mass). We theoretically discuss multi-particle systems where we impose a rigidity constraint, that is, a rigid body of particles. For such a system, the only possible motion relative to the center of mass is rotation. We therefore consider the kinematics of the rigid body frame (the frame which is attached to the rigid body) relative to an inertial frame.
► Next: Moment of Inertia Tensor/Matrix for a Rigid Body | Principal Axis Frame
► Dr. Shane Ross, Virginia Tech professor (Caltech PhD)
► Class lecture notes in PDF form here
► in OneNote form here:
► Textbook used:
Engineering Dynamics: A Comprehensive Introduction
by N. Jeremy Kasdin and Derek A. Paley
Lecture 2020-09-17, Fall 2020
Author's website:
#Multiparticle #energy #AngularMomentum
► Next: Moment of Inertia Tensor/Matrix for a Rigid Body | Principal Axis Frame
► Dr. Shane Ross, Virginia Tech professor (Caltech PhD)
► Class lecture notes in PDF form here
► in OneNote form here:
► Textbook used:
Engineering Dynamics: A Comprehensive Introduction
by N. Jeremy Kasdin and Derek A. Paley
Lecture 2020-09-17, Fall 2020
Author's website:
#Multiparticle #energy #AngularMomentum
Two Particle 2D Example, Energy Approach | Intro to Rigid Body of Particles & Kinematics | Lectu...
Particle in a 2D box (2D infinite potential well)
2D Particle in a box Calculate the energies and draw different states
Particle in a 2D box | Quantum Mechanics | LetThereBeMath |
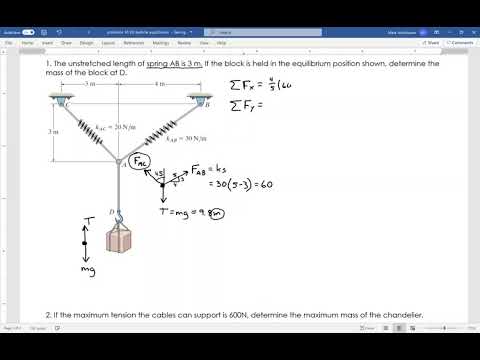
ENGR 220 2D Particle Equilibrium Example 4
ENGR 220 2D Particle Equilibrium Example 1
The Schrödinger Equation Explained in 60 Seconds
Problem 3-18-2D equilibrium of a particle
Single Particle Dynamics | 1D and 2D Worked Examples
How small are atoms?
Energy levels of a 2D particle in a box Sp 2 B2b
Conservation of Momentum In Two Dimensions - 2D Elastic & Inelastic Collisions - Physics Problem...
Particle in a 2-D box wavefunction derivation
What is the Wave/Particle Duality? Part 1
Statics - 2D particle equilibrium example 1
Particle in 2D and 3D box
Lecture 8: Particle in a Two Dimensional Box (Infinite Barrier)
Quantum Chemistry 3.5 - Particle in a Box
Particle in a 2D Box
Brian Cox explains quantum mechanics in 60 seconds - BBC News
Separation of Variables in ODE | Schrödinger Equation: 2D & 3D Particle in a Box
Quantum Degeneracy | Particle in {2D, 3D} Box
Physics 10 Momentum and Impulse (27 of 30) 2-D Collision Ex.1
Dynamics - Lesson 11: Absolute Dependent Motion of Two Particles
Комментарии
 1:07:07
1:07:07
 0:14:40
0:14:40
 0:18:27
0:18:27
 0:19:51
0:19:51
 0:04:11
0:04:11
 0:04:55
0:04:55
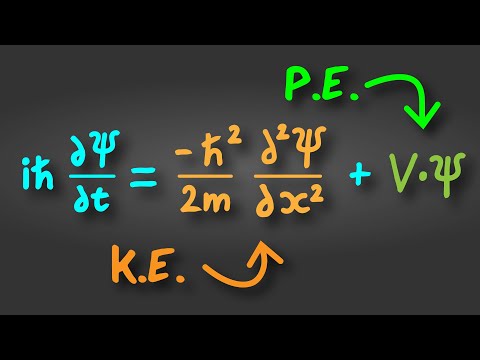 0:01:00
0:01:00
 0:08:17
0:08:17
 0:57:28
0:57:28
 0:00:48
0:00:48
 0:16:24
0:16:24
 0:10:25
0:10:25
 0:22:02
0:22:02
 0:01:07
0:01:07
 0:07:05
0:07:05
 0:14:06
0:14:06
 0:21:42
0:21:42
 0:07:59
0:07:59
 0:31:25
0:31:25
 0:01:22
0:01:22
 0:08:19
0:08:19
 0:03:54
0:03:54
 0:11:27
0:11:27
 0:19:18
0:19:18