filmov
tv
Why The Schrodinger Equation Fails at Relativity

Показать описание
Why did Schrodinger go through with a non-relativistic quantum mechanics, when special relativity was published twenty years before the Schrodinger equation? And how do we know the Schrodinger equation is in fact, non-relativistic?
Klein-Gordon Derivation:
Klein-Gordon Derivation:
Why The Schrodinger Equation Fails at Relativity
The Man Who Saved Quantum Physics When the Schrodinger Equation Failed
Why Relativity Breaks the Schrodinger Equation
The Schrödinger Equation Explained in 60 Seconds
DISCREPANCIES FACED BY SCHRODINGER EQUATIONS || WHY SCHRODINGER EQUATION FAILS IN RELATIVISTIC CASE
'The measurement problem violates the Schrödinger equation' | Roger Penrose on #quantummec...
The Problem with Quantum Measurement
SOLVING the SCHRODINGER EQUATION | Quantum Physics by Parth G
Your Daily Equation #12: The Schrödinger Equation--the Core of Quantum Mechanics
Schrodinger Equation. Get the Deepest Understanding.
Quantum Mechanics and the Schrödinger Equation
Schrödinger's cat: A thought experiment in quantum mechanics - Chad Orzel
The True Meaning of Schrödinger's Equation
Mind Blowing Physics Behind the Schrodinger Equation
Particle in a Box Part 1: Solving the Schrödinger Equation
How to Solve Schrodinger Equation Practice Problems
Space-Time: The Biggest Problem in Physics
Determining the time dependence of the Schrödinger Equation (separation of variables)
Ch 13: Where does the Schrödinger equation come from? | Maths of Quantum Mechanics
Solve the s-wave Schrodinger equation for ground state and first excited state of hydrogen
Schrodinger Equation N-Body Problem
Example Problem Using Wavefunctions and Schrodinger Equation
Griffiths QM Problem 2.3: Prove that Infinite Square Well Can't have E=0 or E less than 0
What the Schrodinger equation truly means: Schrödinger's original derivation
Комментарии
 0:13:02
0:13:02
 0:12:57
0:12:57
 0:17:09
0:17:09
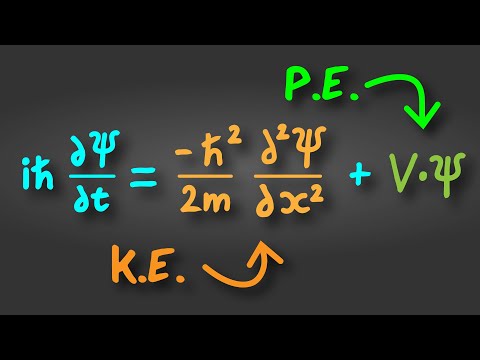 0:01:00
0:01:00
 0:05:39
0:05:39
 0:01:00
0:01:00
 0:06:57
0:06:57
 0:13:04
0:13:04
 0:29:55
0:29:55
 0:49:30
0:49:30
 0:06:28
0:06:28
 0:04:38
0:04:38
 0:12:19
0:12:19
 0:00:44
0:00:44
 0:16:35
0:16:35
 0:26:32
0:26:32
 0:19:42
0:19:42
 0:20:20
0:20:20
 0:14:58
0:14:58
 0:00:16
0:00:16
 0:11:43
0:11:43
 0:10:44
0:10:44
 0:12:25
0:12:25
 0:24:37
0:24:37