filmov
tv
DISCREPANCIES FACED BY SCHRODINGER EQUATIONS || WHY SCHRODINGER EQUATION FAILS IN RELATIVISTIC CASE

Показать описание
LIMITATIONS OF SCHRODINGER EQUATION
The Schrödinger equation, despite its remarkable success in describing quantum systems, faces several challenges and discrepancies:
1. **Non-relativistic Nature**: The Schrödinger equation does not incorporate relativistic effects, which become significant at high speeds or in strong gravitational fields. For accurate predictions in such situations, relativistic quantum mechanics or quantum field theory is needed.
2. **Interpretational Issues**: The interpretation of the wave function in the Schrödinger equation has been a subject of debate, leading to various interpretations like the Copenhagen interpretation, Many-Worlds interpretation, and more. Resolving these interpretational issues remains a challenge.
3. **Measurement Problem**: The Schrödinger equation describes how the wave function evolves over time, but it doesn't provide a clear mechanism for wave function collapse during measurement. This is known as the measurement problem and is central to the interpretation of quantum mechanics.
4. **Complexity with Many-Body Systems**: Solving the Schrödinger equation becomes computationally challenging for systems with many interacting particles, leading to the development of approximation methods like density functional theory and quantum Monte Carlo methods.
5. **Quantum Gravity**: Integrating quantum mechanics with general relativity to form a theory of quantum gravity remains an open problem. The Schrödinger equation does not address the gravitational interaction.
6. **Quantum-Classical Boundary**: Understanding how quantum behavior emerges from classical mechanics at the macroscopic scale, known as the quantum-classical boundary problem, is not fully addressed by the Schrödinger equation alone.
Despite these challenges, the Schrödinger equation has been incredibly successful in describing and predicting the behavior of quantum systems in a wide range of scenarios.
1. Quantum Mechanics
2. Schrödinger Equation
3. Quantum Theory
4. Wave Function
5. Relativistic Effects
6. Measurement Problem
7. Interpretations of Quantum Mechanics
8. Many-Body Systems
9. Quantum Gravity
10. Quantum-Classical Boundary
1. **What:** What are the typical boundary conditions used in solving Schrödinger equations?
2. **Why:** Why do discrepancies sometimes arise between theoretical predictions based on Schrödinger equations and experimental observations in quantum mechanics?
3. **Where:** Where in the solution process of Schrödinger equations do approximation methods often introduce discrepancies?
4. **When:** When do discrepancies between different interpretations of solutions to Schrödinger equations become significant in quantum mechanics?
5. **Who:** Who are the researchers or theorists who have contributed significantly to addressing discrepancies in Schrödinger equation solutions?
6. **Which:** Which experimental setups or scenarios commonly highlight discrepancies between theoretical predictions and observed outcomes based on Schrödinger equations?
7. **How:** How do discrepancies in boundary conditions affect the solutions of Schrödinger equations and their physical interpretations?
These questions can help explore various aspects of discrepancies encountered in the context of Schrödinger equations and their implications in quantum mechanics.
#quantumtunneling
#quantumentanglement
#collapseofwavefunction
#negativeenergyremoval
The Schrödinger equation, despite its remarkable success in describing quantum systems, faces several challenges and discrepancies:
1. **Non-relativistic Nature**: The Schrödinger equation does not incorporate relativistic effects, which become significant at high speeds or in strong gravitational fields. For accurate predictions in such situations, relativistic quantum mechanics or quantum field theory is needed.
2. **Interpretational Issues**: The interpretation of the wave function in the Schrödinger equation has been a subject of debate, leading to various interpretations like the Copenhagen interpretation, Many-Worlds interpretation, and more. Resolving these interpretational issues remains a challenge.
3. **Measurement Problem**: The Schrödinger equation describes how the wave function evolves over time, but it doesn't provide a clear mechanism for wave function collapse during measurement. This is known as the measurement problem and is central to the interpretation of quantum mechanics.
4. **Complexity with Many-Body Systems**: Solving the Schrödinger equation becomes computationally challenging for systems with many interacting particles, leading to the development of approximation methods like density functional theory and quantum Monte Carlo methods.
5. **Quantum Gravity**: Integrating quantum mechanics with general relativity to form a theory of quantum gravity remains an open problem. The Schrödinger equation does not address the gravitational interaction.
6. **Quantum-Classical Boundary**: Understanding how quantum behavior emerges from classical mechanics at the macroscopic scale, known as the quantum-classical boundary problem, is not fully addressed by the Schrödinger equation alone.
Despite these challenges, the Schrödinger equation has been incredibly successful in describing and predicting the behavior of quantum systems in a wide range of scenarios.
1. Quantum Mechanics
2. Schrödinger Equation
3. Quantum Theory
4. Wave Function
5. Relativistic Effects
6. Measurement Problem
7. Interpretations of Quantum Mechanics
8. Many-Body Systems
9. Quantum Gravity
10. Quantum-Classical Boundary
1. **What:** What are the typical boundary conditions used in solving Schrödinger equations?
2. **Why:** Why do discrepancies sometimes arise between theoretical predictions based on Schrödinger equations and experimental observations in quantum mechanics?
3. **Where:** Where in the solution process of Schrödinger equations do approximation methods often introduce discrepancies?
4. **When:** When do discrepancies between different interpretations of solutions to Schrödinger equations become significant in quantum mechanics?
5. **Who:** Who are the researchers or theorists who have contributed significantly to addressing discrepancies in Schrödinger equation solutions?
6. **Which:** Which experimental setups or scenarios commonly highlight discrepancies between theoretical predictions and observed outcomes based on Schrödinger equations?
7. **How:** How do discrepancies in boundary conditions affect the solutions of Schrödinger equations and their physical interpretations?
These questions can help explore various aspects of discrepancies encountered in the context of Schrödinger equations and their implications in quantum mechanics.
#quantumtunneling
#quantumentanglement
#collapseofwavefunction
#negativeenergyremoval
 0:05:39
0:05:39
 0:07:46
0:07:46
 0:11:09
0:11:09
 0:12:19
0:12:19
 0:04:34
0:04:34
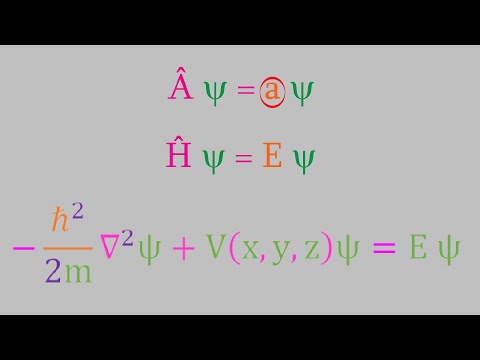 0:16:53
0:16:53
 0:55:36
0:55:36
 0:43:33
0:43:33
 0:12:59
0:12:59
 0:17:56
0:17:56
 0:52:23
0:52:23
 0:25:18
0:25:18
 0:46:00
0:46:00
 0:11:25
0:11:25
 0:25:18
0:25:18
 1:01:56
1:01:56
 0:24:04
0:24:04
 1:08:58
1:08:58
 1:15:31
1:15:31
 0:08:56
0:08:56
 2:01:25
2:01:25
 0:18:36
0:18:36
 0:14:47
0:14:47
 0:14:16
0:14:16