Proof: Infimum of {1/n} = 0 | Real Analysis

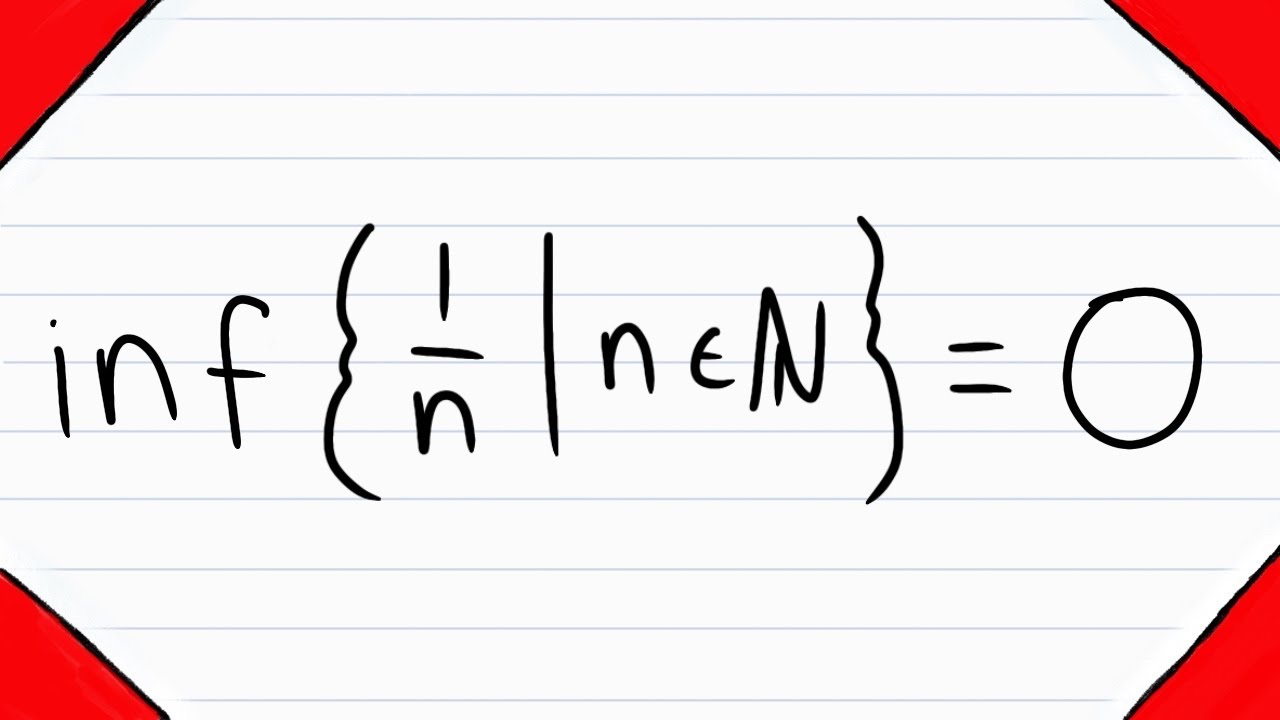
Показать описание

The infimum of the set containing all reciprocals of natural numbers has an infimum of 0. That is, 0 is the greatest lower bound of {1/n | n is natural}. We prove this infimum in today's real analysis lesson using the Archimedean Principle, which tells us that given any real number x, we can find a greater natural number.

Thanks to Nasser Alhouti, Robert Rennie, Barbara Sharrock, and Lyndon for their generous support on Patreon!

I hope you find this video helpful, and be sure to ask any questions down in the comments!

+WRATH OF MATH+

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

preparing for my exam and it's the first part of what we learned this term, seems my mind is blank... Thank you for your video!

annali

Wonders my situation if these lectures weren't there

antebantesaathmaintante

I think that if we want to divide by n both sides in the inequality 0<=1 we must first assure that n is not equal to zero, as zero belongs to N set.

ioannis

2:54 You forgot to mention that n must be greater or equal to 0
n can't be negative

RazorM

1/Epsilon does not belong to the set of real number since it doesn’t include 0 and the negatives so that mean the archamdian property does not apply. Right?

Rayglobster

thank you for these videos I am 9th a 9th grader who really wants to learn real analysis but the problem is just reading the book dosen't help me understand as much as these videos do also any suggestions on how I could self-teach myself such kinds of stuff where I cannot just sit read the book and understand what's going on

adityaekbote

My favorite part is when you use the first order symbols! I've never used them so "Backwards E, x, curved E, R with an extra line, such that, x >= n, upside down A, n, curved E, N with an extra line..." sounds like a new language! How did you go about learning to use these symbols?

cheatyhotbeef

You can also just start with n>0 because n is a natural number. The lowest natural number is 1, and obviously 1>0.
So (1/n)>0, dividing both sides by n. This shows 0 is a lower bound.

garyanderson

S={sin (nπ/6 ;n belong to natural number}.sir tell me suprimum

manahilfatima

Hey I just wanna say all this stuff is really fucking useful for students! I’m watching this to cram for my proofs final in a few hours, and tysm for this work

rbran

Why that o is a lower bound of the set??

eddiemoring

Proof: Infimum of {1/n} = 0 | Real Analysis

Proof: Supremum of {n/(n+1)} = 1 | Real Analysis

Proof: Infimum of {1/n} = 0 | Real Analysis

Proof: Supremum of {1/n} = 1 | Real Analysis

Sup(1- 1/n), n is natural number | Sup(A) and Inf(A) | Use of Archimedean Property

Definition of Supremum and Infimum of a Set | Real Analysis

Proof: Supremum and Infimum are Unique | Real Analysis

Show that Inf(1/n)=0

Real Analysis 6 | Supremum and Infimum

Proof: Minimum of a Set is the Infimum | Real Analysis

2.5 Supremum: proof - sup(0,1)=1

Showing that the Infimum of {X,Y} Exists in the Partial Order [ Ƥ(M), ⊆ ]

Supremum and infimum of a set

Intro to Real Analysis - Video 6: ex of proof showing sup{1/n}=1 and inf{1/n}=0

Inf of {1/n} using Archimedean Property

Epsilon Definition of Supremum and Infimum | Real Analysis

Examples Of Supremum And Infimum I Real Analysis I BSc Maths I Engg Maths

How to use the epsilon definition of sup in a proof

Example 1 of Finding Supremum and Infimum

How to use Definition 1 of Sup in a proof

Real Analysis | The Supremum and Completeness of ℝ

Mathematical Analysis Class 20: Supremum and Infimum

Prove Infimums Exist with the Completeness Axiom | Real Analysis

Proof! sup(1-1/n)=1 (Real Analysis)

Proof: Sequence 1/n Converges to 0 | Real Analysis Exercises