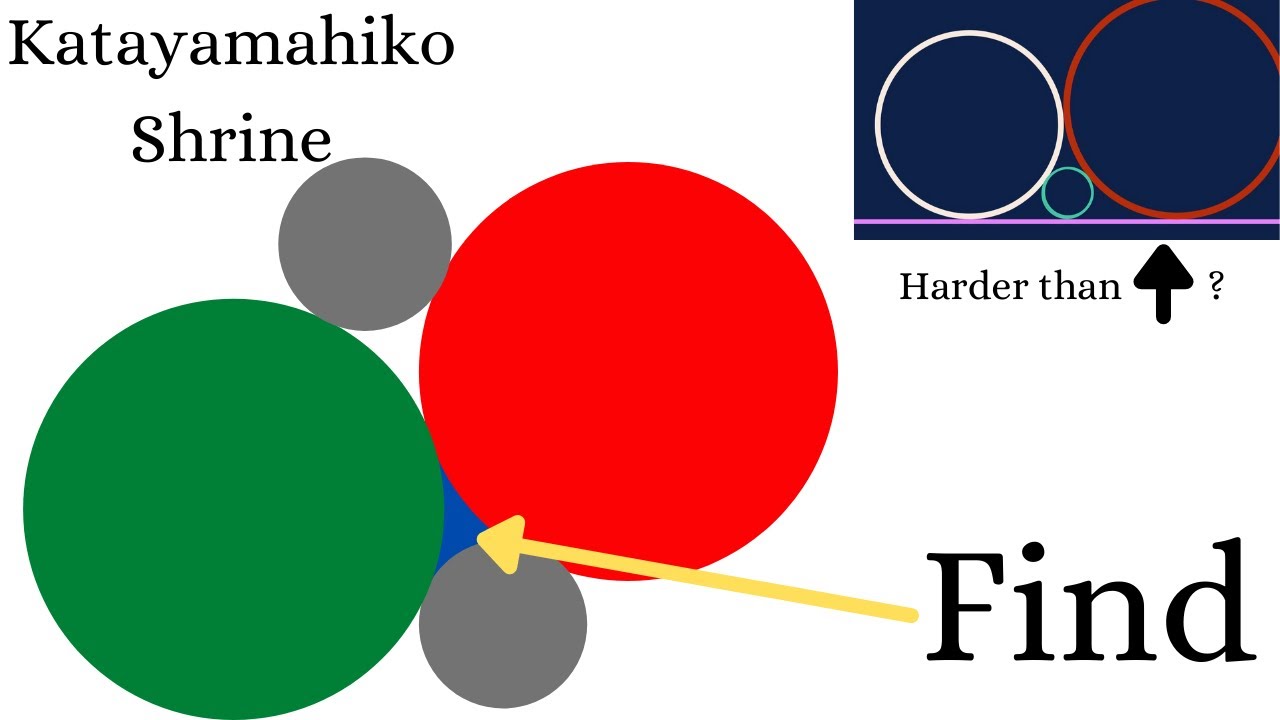
An 1800s Japanese circle problem!

If you are going to use an ad-blocker, considering using brave and tipping me BAT!

Books I like:

Abstract Algebra:

Differential Forms:

Number Theory:

Analysis:

Calculus:

My Filming Equipment:

[aswinibanerjee]

Technically the thumbnail was a clickbait

[Bodyknock]

I like rewriting r = √2 / (√2 + 1) by multiplying top and bottom by the conjugate (√2 - 1), which gives the nicer looking answer r = 2 - √2. 🙂

[goodplacetostop]

5:36 Michael’s homework
6:16 それはいいところで止まっている

[OscarCunningham]

You can rationalise the denominator to get the simpler expression r = 2 - √2.

[seroujghazarian]

Let a be the side length of the square.
Half of the diagonal=1+sqrt(2)
a×sqrt(2)/2=1+sqrt(2)
a=2+sqrt(2)

[manucitomx]

I love this kind of geometry problems.
Thank you, professor!

[gugdigrazia]

Great video! Are you going yo upload other Physics Olympiad problems in the future?

[mrflibble]

Thank you again Michael.
Your work is much appreciated, and the detail shown in your solutions is exceptional.

[wisarutsuwanprasert]

I like how different colors were used to indicate different segments.

[mathflipped]

This is a really cool problem! I never liked geometry problems on the olympiads.

[emersonschmidt]

The circle with x radius is inside an isosceles triangle with two sides equal to r+r*sqrt(2). Drawing a parallel to one of the straight lines inside the square through the center of the circle with x radius, we get other isosceles triangle with equal sides that can be calculated in two diferent ways: r-x+r*sqrt(2) and . Equating both expressions and simplifying permits the calculation of x:
By doing t=sqrt(x) we get a second degree equation whose (useful) solution is
Therefore r=t^2 which is approx. 0.26

[backyard]

if diagonal of the square is d and it's sidelength is a, then by pythagorean theorem a^2+a^2=d^2, i.e. d=a*sqrt(2).
but from the picture d = 2*(1+sqrt(2)), so the sidelength a = 2*(1+sqrt(2)) / sqrt(2). Also, 2/sqrt(2) is equal to just sqrt(2). so a=sqrt(2) * (1+sqrt(2)) = 2 + sqrt(2).

[norbi]

my take on the homework:

both circles' centers lie on the angle bisector of the upper angle, and we will construct two additional triangles ∆R and ∆X, which both share a point with the upper angle of the big triangle, have points in the circles' centers, and the last one on the diagonal side

triangles are similar with a scale of x/r

we can get the measurements by noticing another 45°-45°-90° right triangle, and seeing that the side of the ∆R on the diagonal is equal to r+r√2

∆R side lengths are therefore
r ; r(√2+1) ; r√(4+2√2)

the third side length is of particular interest, and in the ∆X is equal x√(4+2√2) due to scale

but then we can see that

r√(4+2√2) = r + x√(4+2√2)

and therefore:

x = r(1 - 1/√(4+2√2))

as a bonus, were we to draw another, even smaller circle, with a radius y, the ratio of y to x would be the same as the x to r, and thus we can get a nice fractal

as a matter of fact, were we to add all of the radiuses, we get a nice geometric sum

r/(1-(1-1/√(4+2√2))) = r√(4+2√2)

[akrickok]

It always seems to me with these geometry problems that we take a lot of things for granted, for example, the fact that the larger circles share a point which happens to be the center of the square. I think it would be better to prove or at least sketch a proof for each solving step, like you do most of the time in your number theory videos, for example. Still enjoyed the video, though :)

[andreivila]

The side length of the square is 2+sqrt(2) because we know the diagonal. Not x is trickier… We can calculate in two ways the length of the bisector in the small isosceles right angled triangle. We would get (2-sqrt(2))/sin(pi/8) since r=2-sqrt(2) from rationalizing. But in the same way we get 2-sqrt(2)+x+x/sin(pi/8). So Dividing by 1+csc(pi/8) gives out x. Of course, since we know sin and cos of pi/4, one can calculate sin and cos of pi/8 rather easily.

[DrQuatsch]

The square has sides 2 + sqrt(2). The diagonal is twice the semi-diagonal, so 2 * (1 + sqrt(2)) = 2*sqrt(2) + 2. The diagonal of the square is sqrt(2) bigger than the sides, so the sides are (2*sqrt(2) + 2) / sqrt(2) = 2 + sqrt(2). Interestingly you can simplify the radius of the small circle as well, by multiplying top and bottom by the conjugate and then you get 2 - sqrt(2), which is the conjugate of the side of the square. [sqrt(2) * (sqrt(2) - 1)] / [(1 + sqrt(2)) * (sqrt(2) - 1)] = [2 - sqrt(2)]/1 = 2 - sqrt(2)

[emanuellandeholm]

Love these geometry problems professor Penn! :)

[idomeir]

Hi I have a suggestion for a problem.

Find all non negative integers n such that there are positive integers a, b such that
n!=2^a+2^b

[robberbarron]

I showed my mom the exact same diagonal of a square when telling her why an office space with side lengths 24% of the apartment space has more like 50% in ft^2

[gtziavelis]

thumbnail is a slightly different problem