filmov
tv
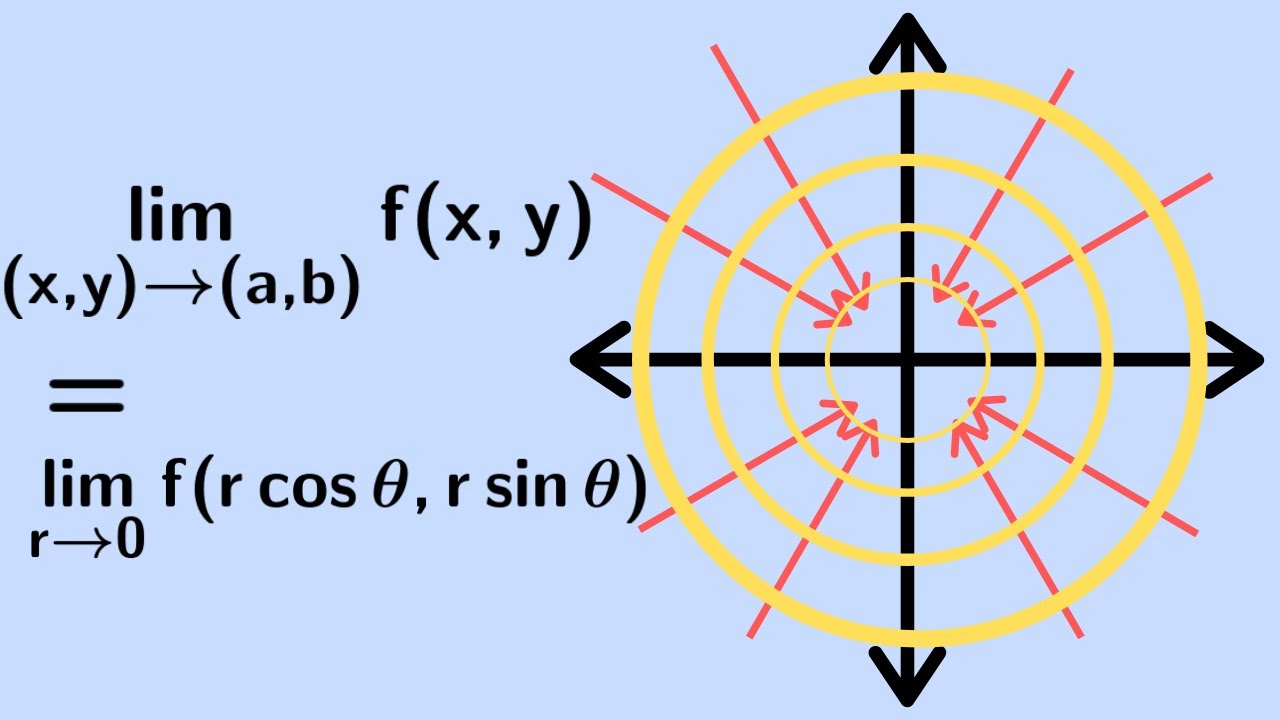
Multivariable Calculus | Finding a limit with polar coordinates.
Показать описание
We use polar coordinates to find the limit of a multivariable function.
❖ Multivariable Calculus: Finding and Sketching the Domain ❖
Multivariable Calculus | Finding a limit with polar coordinates.
Calculus 3 Lecture 13.1: Intro to Multivariable Functions (Domain, Sketching, Level Curves)
Limits of Multivariable Functions - Calculus 3
Partial Derivatives - Multivariable Calculus
Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3
Multivariable maxima and minima
Limits are...weird...for multi-variable functions | Limits along paths
Calculus 3 Lecture 13.2: Limits and Continuity of Multivariable Functions (with Squeeze Th.)
domain of a multivariable function (KristaKingMath)
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Equations of Planes: Vector & Component Forms | Multivariable Calculus
Multivariable Calculus | Finding the equation of a tangent plane.
critical points of multivariable functions (KristaKingMath)
14.1 Domain and range for multi-variable functions
How to find the TANGENT PLANE | Linear approximation of multi-variable functions
Local extrema and saddle points of a multivariable function (KristaKingMath)
Calculus 3 Lecture 13.4: Finding Differentials of Multivariable Functions
Multivariable Optimization with Boundaries
Multivariable Calculus Final Exam Review
The Vector Equation of Lines | Multivariable Calculus
Epic Multivariable Calculus Workbook
Chain Rule With Partial Derivatives - Multivariable Calculus
Finding a Potential for a Conservative Vector Field
Комментарии
 0:06:21
0:06:21
 0:03:04
0:03:04
 1:49:07
1:49:07
 0:19:04
0:19:04
 1:00:33
1:00:33
 0:14:35
0:14:35
 0:08:04
0:08:04
 0:05:38
0:05:38
 2:14:36
2:14:36
 0:05:37
0:05:37
 0:11:24
0:11:24
 0:04:28
0:04:28
 0:04:50
0:04:50
 0:05:25
0:05:25
 0:10:45
0:10:45
 0:09:23
0:09:23
 0:11:23
0:11:23
 1:51:04
1:51:04
 0:15:08
0:15:08
 1:17:35
1:17:35
 0:05:30
0:05:30
 0:00:55
0:00:55
 0:21:10
0:21:10
 0:10:07
0:10:07