filmov
tv
Olympiad Geometry Problem #34: IMO Shortlist 2002 G7
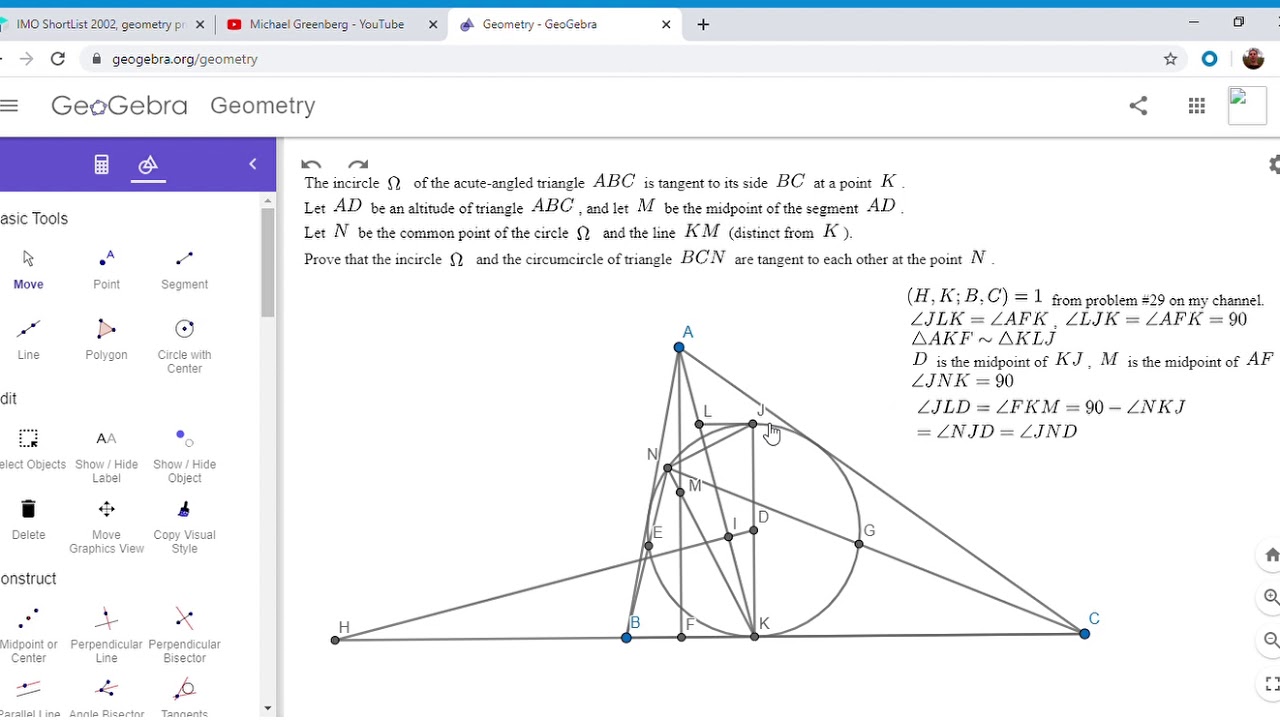
Показать описание
This is such a beautiful and deep problem, only a few lines and you have to prove two circles are tangent, and yet it's very tricky! It's from the 2002 IMO Shortlist. Link below.
0:17:07
Olympiad Geometry Problem #34: IMO Shortlist 2002 G7
0:01:00
A beautiful international math olympiad problem
0:00:34
Chinese IMO team
0:10:58
Olympiad Geometry Problem #37: IMO 2018 #1
0:00:37
When mathematicians get bored (ep1)
0:00:59
Oxford Student reacts to China’s INSANELY DIFFICULT High School GaoKao Maths paper #shorts #viral
1:32:45
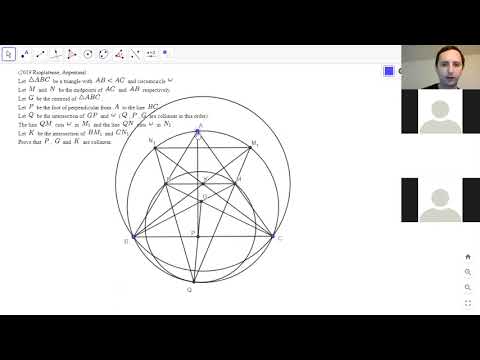
LIVESTREAM GEO#34A: Speeding Through the Rioplatenese Olympiad!
0:08:42
Olympiad Geometry Problem #43: IMO 2017 #4
0:11:01
Olympiad Geometry Problem #102: Orthocenter, Equal Segments, Bisection
0:08:45
The Legend of Question Six - Numberphile
0:09:04
Olympiad Geometry Problem #33: Incenter, Angle Bisector, Midpoint
0:02:34
A Nice Math Olympiad Exponential Equation 3^x = X^9
0:35:27
AlphaGeometry: Solving olympiad geometry without human demonstrations (Paper Explained)
0:09:51
Olympiad Geometry Problem #58: IMO 2013 #4
0:07:54
Olympiad Geometry Problem #100: Circumcenter Perpendiculars Cyclic Quad
0:11:20
Olympiad Geometry Problem #65: IM Lemma
0:11:13
IMO Challenge Problem - International Mathematical Olympiad
0:21:37
Olympiad Geometry Problem #84: IMO Shortlist 2012 G6
0:08:17
Olympiad Geometry Problem #78: Incenter, Midpoint, Parallel
0:00:50
5 simple unsolvable equations
0:00:34
My math olympiad rank #shorts #maths
0:14:46
Olympiad Geometry Problem #86: IMO Shortlist 2019 G2
0:00:13
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
0:17:04
Olympiad Geometry Problem #74: Incircle, Equal Segments, Right Angle
Комментарии