filmov
tv
Olympiad Geometry Problem #100: Circumcenter Perpendiculars Cyclic Quad
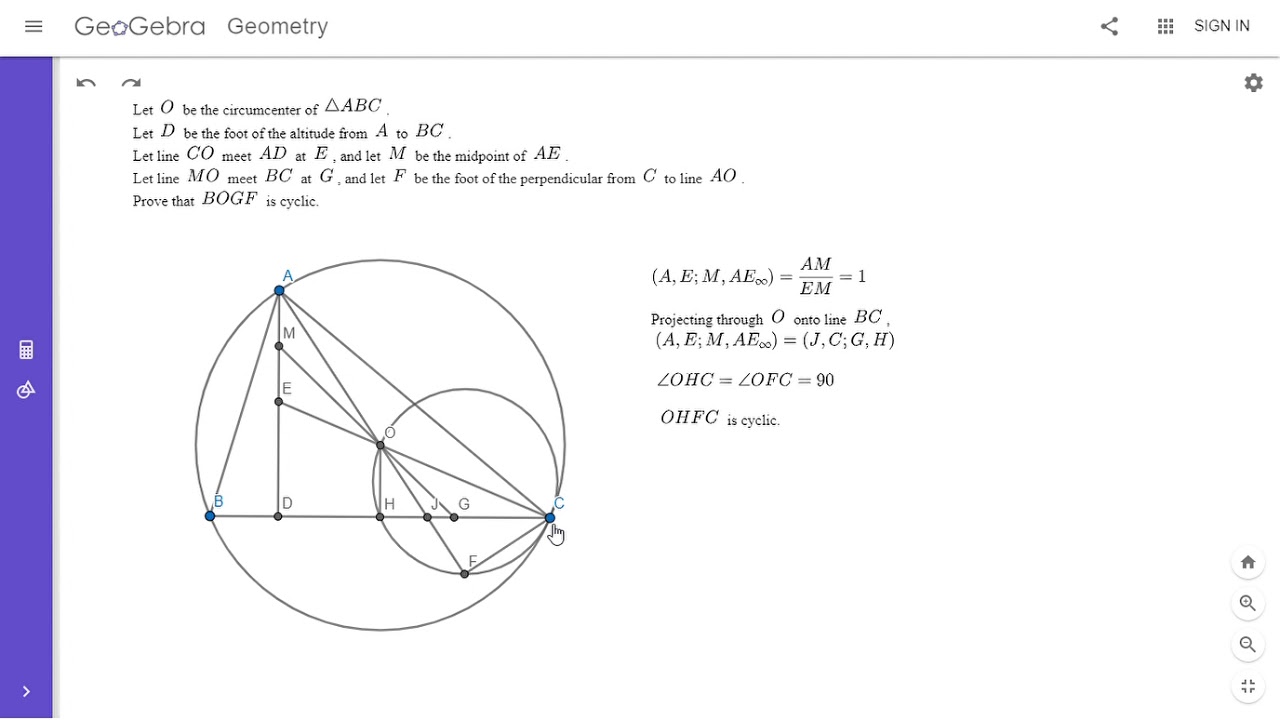
Показать описание
Here is a tremendous problem from the 2010 Kazakhstan Math Olympiad, recommended to me by another subscriber on my channel. It was a nice challenge, although still probably easier than some of my more recent videos. Enjoy! Link below.
Olympiad Geometry Problem #100: Circumcenter Perpendiculars Cyclic Quad
#1shorts. Archimedes lemma
Olympiad Geometry Problem #35: Angle Bisector, Perpendiculars, Tangency
Olympiad Geometry Problem #23: Orthocenter, Tangent, Equal Segments
Olympiad Geometry Problem #22: Perpendiculars, Parallel, Cyclic
Olympiad Geometry Problem #42: Isosceles Triangle, Median, Altitude, Midpoint
Olympiad Geometry Problem #70: Cyclic Quad, Equal Segements, Perpendicuar
Olympiad Geometry Problem #110: Similar to Video #89 but Much Harder!
Olympiad Geometry Problem #89: Reflections, Tangents, Perpendicular
Olympiad Geometry Problem #20: Orthocenter, Angle Bisector, Tangent
Olympiad Geometry Problem #17: Blanchett's Theorem
Olympiad Geometry Problem #96: Spiral Similarities
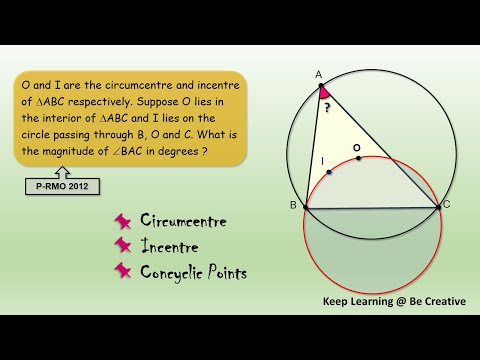
Finding Angle BAC using Circumcenter and Incenter Properties #importantconcept #olympiadmathematics
INMO 2021 Problem 5 | Math Olympiad Geometry
Cyclic Quadrilaterals| Angle Chasing| The Ultimate Geo Course
Geometry | Mathematical Olympiads | Cyclic Quadrilateral | Congruent Triangle | Mid Point Theorem
The SAT Question Everyone Got Wrong
MATH OLYMPIAD | GEOMETRY | COMPETENCY BASED | TRIANGLES |
Circumcenter is Orthocenter of Medial triangle with GXWeb
Most💯 Important Step Before any Procedure 🔥
Nice Geometry Problem From Poland! | Laid Back Math, Episode 48
CIRCUMCENTER OF A TRIANGLE AND THE PROPERTIES @mindurmath .
LIVESTREAM GEO #44A: One of the Hardest Problems Solved on Livestream!
PRMO 2021 - CIRCUMCENTER | Maths Olympiad 2021 | Pre RMO | Pre RMO Preparation | Abhay Mahajan | VOS
Комментарии
 0:07:54
0:07:54
 0:00:25
0:00:25
 0:10:33
0:10:33
 0:08:47
0:08:47
 0:12:37
0:12:37
 0:13:46
0:13:46
 0:11:22
0:11:22
 0:19:03
0:19:03
 0:22:52
0:22:52
 0:13:09
0:13:09
 0:11:39
0:11:39
 0:12:31
0:12:31
 0:02:48
0:02:48
 0:07:30
0:07:30
 0:18:52
0:18:52
 0:08:10
0:08:10
 0:18:25
0:18:25
 0:06:19
0:06:19
 0:03:18
0:03:18
 0:00:16
0:00:16
 0:13:38
0:13:38
 0:57:04
0:57:04
 1:47:48
1:47:48
 1:47:00
1:47:00